O que é?
Uma função logarítmica de base a é uma função escrita na forma f(x)=loga x, sendo a um número positivo, diferente de um e maior que zero.Importante ressaltar que o logaritmo de um número é o expoente x pelo qual precisa se elevar uma base fixa a para obter o número b, tal como na imagem abaixo. Ou seja:
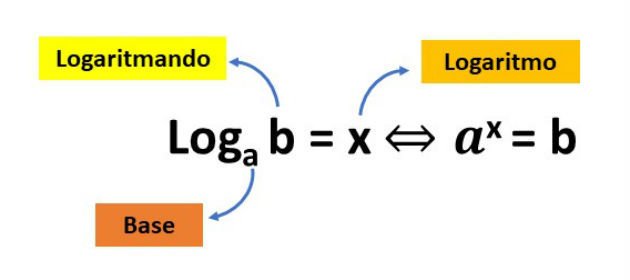
Fonte:https://www.todamateria.com.br/funcao-logaritmica/
Exemplos:
f(x)= log2 x
f(x)= log0,5 x
f(x)=log (x-6) x
Observação: O inverso da função logarítmica é a função exponencial.
Domínio da função logarítmica:
O domínio de uma função representa os valores de x pelos quais a função é definida. Na função logarítmica, o domínio delas deve respeitar as condições de existência do logaritmo.
Com isso, a base e o logaritmando deve números positivos e diferentes de 1.
Exemplo:
Determine o domínio da função:
Log(x-2) (4 - x)
O domínio da função deve respeitar três condições:
I) x - 2> 0
x> 0 +2
x>2
II) 4 - x > 0
-x > 0 -4
-x> -4
(-1) -x > -4 (-1)
(-1) -x > -4 (-1)
x < 4
III) x - 2 ≠ 1
x ≠ 1 + 2
x ≠ 3
Resposta:{x ∈ R| 2< x <3 e 3 < x <4}
III) x - 2 ≠ 1
x ≠ 1 + 2
x ≠ 3
Resposta:{x ∈ R| 2< x <3 e 3 < x <4}
Gráficos:
Para que seja possível construir o gráfico de uma função logarítmica, é preciso que sejam analisadas duas situações:
a>1 (base maior que um)
Função crescente:
Quando uma função logarítmica é crescente, significa que a sua base é maior que 1 e que quando o valor de x, o da imagem aumenta também. (loga x2 > loga x1)
Para que isso seja comprovado, basta atribuir valores para x e calcular a imagem da função.
Função decrescente:
Quando uma função logarítmica é decrescente, significa que a sua base é maior que 0 e menor que 1 e que quando o valor de x aumenta, o da imagem diminui. (loga x1 > loga x2).
Do mesmo modo que se constrói o gráfico de uma função logarítmica crescente, basta atribuir valores para x e calcular a imagem da função.
Características do gráfico da função logarítmica:
* O gráfico sempre passa pelo ponto (1,0) do plano cartesiano, pois o logaritmo sempre será zero.
* O gráfico só passa pela direita do eixo y, pois ela é definida para x > 0.
* Como mencionado, a função inversa logarítmica é a função exponencial, sendo esta última definida como f(x)= a^x, onde a é um número real positivo e diferente de um.
Os gráficos destas funções inversas são simétricas em relação a bissetriz dos quadrantes I e III.
Isso é importante porque ao conhecer o gráfico de uma função logarítmica, é possível construir um gráfico de uma função exponencial através de simetria entre as duas funções.
* Toda vez que aparecer log x, sem indicar a base em relação a qual se torna logaritmo, log x será entendido como log10 x
Dominando o conhecimento - Exercícios:
Questão 1) Os valores de x que satisfazem a log x + log (x-5)= log 36 são:
a) 9 e -4
b)9 e 4
c) -4
d) 9
e) -5 e 4
Questão 2) Uma pessoa aplicou a importância de R$ 500,00 em uma instituição bancária que paga juros mensais de 3,5% no regime de juros compostos. Quanto tempo após a aplicação o montante será de R$ 3500,00?
* Se necessário use log 1,035=0,0149, log 7= 0,8451
* Se necessário use log 1,035=0,0149, log 7= 0,8451
Questão 3) Estabeleça o domínio das seguintes funções:
a)y= log3 (x- 1/2)
b)y=log(x-1) (-3x + 9)
c)y= log(x + 2) (x^2 - 4)
Questão 4) (PUC) Assinale a alternativa válida sempre:
a) log (a • b)= log a • log b
b) log (a + b)= log a + log b
c)log m • a= m • log a
d)log a^m= log m • a
e)log a^m= m • log a
b) log (a + b)= log a + log b
c)log m • a= m • log a
d)log a^m= log m • a
e)log a^m= m • log a
Resolução:
Questão 1)
I) Ao aplicar a propriedade de um logaritmo de um produto, obtemos a seguinte relação:
log [x(x-5)]=log 36
log (x^2 -5x)=log 36
II) Como as bases dos logaritmos são iguais, os logaritmandos também são iguais e a equação se desenvolve da seguinte forma:
x^2 - 5x=36
x^2 - 5x -36=0
Coeficientes da equação
a=1
b= -5
c= -36
Coeficientes da equação
a=1
b= -5
c= -36
III) Como a equação desenvolvida é uma do segundo grau, poderá ser resolvida através da fórmula de Bhaskara:
∆=b^2 - 4ac
∆= (-5)^2 - 4 • 1• (-36)
∆=25 + 144
∆=169
x= -b ± √∆
∆= (-5)^2 - 4 • 1• (-36)
∆=25 + 144
∆=169
x= -b ± √∆
2a
x=-(-5)± √169
2 • 1
x= 5 ± 13
2
x'= 5 + 13
2
x'= 18
2
x'=9
x''= 5 - 13
2
x''= - 8
2
x''= -4
IV) Considerando que, para a equação ser satisfeita, x precisa ser maior que zero (x > 0). Portanto, o único valor que satisfaz a equação é nove.
Resposta:Item d
Questão 2)
I) O montante que resulta do tempo de aplicação dos juros compostos é dado pela seguinte expressão:
M=C0 • (1 + i)^t
Onde:
M(montante)= R$ 3500,00
C0 (capital inicial)= R$ 500,00
i=3,5%=0,035
t=?
II) Substituindo os termos da expressão por seus respectivos valores numéricos, temos que:
3500= 500 • (1 + 0,035)^t
x=-(-5)± √169
2 • 1
x= 5 ± 13
2
x'= 5 + 13
2
x'= 18
2
x'=9
x''= 5 - 13
2
x''= - 8
2
x''= -4
IV) Considerando que, para a equação ser satisfeita, x precisa ser maior que zero (x > 0). Portanto, o único valor que satisfaz a equação é nove.
Resposta:Item d
Questão 2)
I) O montante que resulta do tempo de aplicação dos juros compostos é dado pela seguinte expressão:
M=C0 • (1 + i)^t
Onde:
M(montante)= R$ 3500,00
C0 (capital inicial)= R$ 500,00
i=3,5%=0,035
t=?
II) Substituindo os termos da expressão por seus respectivos valores numéricos, temos que:
3500= 500 • (1 + 0,035)^t
3500 = (1 + 0,035)^t
500
7= 1,035^t
III) Aplicando o logaritmo nos dois lados da equação temos:
log 1,035^t= log 7
t • log 1,035= log 7
t • 0,0149= 0,8451
t= 0,8451
0,0149
t=56,7 meses
Resposta: O montante será de R$ 3500,00 após 56,7 meses de aplicação.
Questão 3)
a)y= log3 (x- 1/2)
I) O domínio da função precisa respeitar uma única condição que é:
x - 1/2 > 0
x> 0 + 1/2
x>1/2
D={x ∈ R| x > 1/2}
b)y=log(x-1) (-3x + 9)
I) Para esta função, existem três restrições:
II) x - 1 > 0
x > 0 +1
x > 1
III) -3x + 9 >0
-3x > -9
3x < 9
x < 9/3
x < 3
IV) x - 1≠ 1
x≠ 1 +1
x≠ 2
Resposta:D={x ∈ R| 1< x <2 e 2 < x < 3}
c)y= log(x + 2) (x^2 - 4)
I) Para esta função, existem três restrições:
II) x + 2 > 0
x > 0 - 2
x > -2
III) x^2 - 4 >0
x^2 > 4
x >±√4
x > 2
x < -2
IV) x + 2≠ 1
x≠ 1 -2
x≠ -1
Resposta:D={x ∈ R| x >2 ou x ≠ -1 }
Questão 4) Resposta: Item e.
3-https://brasilescola.uol.com.br/matematica/funcao-logaritmica.htm
4-https://www.todamateria.com.br/funcao-logaritmica/
5-https://mundoeducacao.bol.uol.com.br/matematica/funcao-logaritmica.htm
6-https://mundoeducacao.bol.uol.com.br/matematica/equacao-logaritmica-ii.htm
7-https://www.infopedia.pt/$funcao-logaritmica
8-http://no-mundo-da-matemagica.blogspot.com/2013/07/problemas-de-logaritmos-envolvendo-o.html
9-https://www.coladaweb.com/exercicios-resolvidos/exercicios-resolvidos-de-matematica/funcao-logaritmica-e-exponencial
Agradecimentos:
Agradeço a todos que prestigiaram meu blog e espero que gostem das atuais e futuras postagens do blog. Quem tiver dúvidas, pode comentá-las. Espero ter ajudado.
Referências:
2-https://exercicios.brasilescola.uol.com.br/exercicios-matematica/exercicios-sobre-funcao-logaritmica.htm3-https://brasilescola.uol.com.br/matematica/funcao-logaritmica.htm
4-https://www.todamateria.com.br/funcao-logaritmica/
5-https://mundoeducacao.bol.uol.com.br/matematica/funcao-logaritmica.htm
6-https://mundoeducacao.bol.uol.com.br/matematica/equacao-logaritmica-ii.htm
7-https://www.infopedia.pt/$funcao-logaritmica
8-http://no-mundo-da-matemagica.blogspot.com/2013/07/problemas-de-logaritmos-envolvendo-o.html
9-https://www.coladaweb.com/exercicios-resolvidos/exercicios-resolvidos-de-matematica/funcao-logaritmica-e-exponencial

Nenhum comentário:
Postar um comentário