Função afim

O que é?

Uma função afim, também conhecida como função do primeiro grau, é toda função f: R => R escrita na forma f(x)=ax + b, sendo que a,b ∈ R.
Neste tipo de função, a é o coeficiente de x e indica a taxa de crescimento, ou variação, da função.
O número b é conhecido como termo constante ou coeficiente linear.
Exemplos:
y=2x + 1
y=2x

                            

Raiz da função afim:

A raiz da função afim é o ponto no qual o gráfico da função intercepta o eixo x, ou seja, o ponto no qual f(x)=0. Por isso, para descobrir a raiz de uma função afim, basta substituir f(x) por 0. Com isso temos a seguinte relação:

f(x)=ax +b

0= ax +b

ax= -b

x= - b/a

                   
Fonte:https://www.stoodi.com.br/blog/2018/06/13/funcao-afim/

Gráfico de uma função afim:

O gráfico descrito por uma função afim é uma reta oblíqua aos eixos x e y. A reta não pode ser perpendicular a nenhum dos eixos. Os fatores que vão determinar a inclinação e direção da reta são os coeficientes angular(a) e linear da função(b). 
Para escrever o gráfico destas funções, basta atribuir valores para x e calcular o valor da imagem.

                ~
Fonte:https://blog.maxieduca.com.br/tipos-funcao-plinomial/imagem-5-2/

Coeficiente angular e linear:

O coeficiente angular a da função afim indica a inclinação da reta em relação ao eixo das abscissas. 

Já o coeficiente b, ou coeficiente linear, representa o ponto onde x=0. Porque sendo x=0, temos que:

y=ax + b

y= a • 0 + b
y=b

O coeficiente linear indica o ponto onde a reta corta o eixo y.

Função linear:

É toda função na qual b=0, com a≠0. Ela sempre passa pelo ponto (0,0). A fórmula da função afim é escrita como:

f(x)= ax

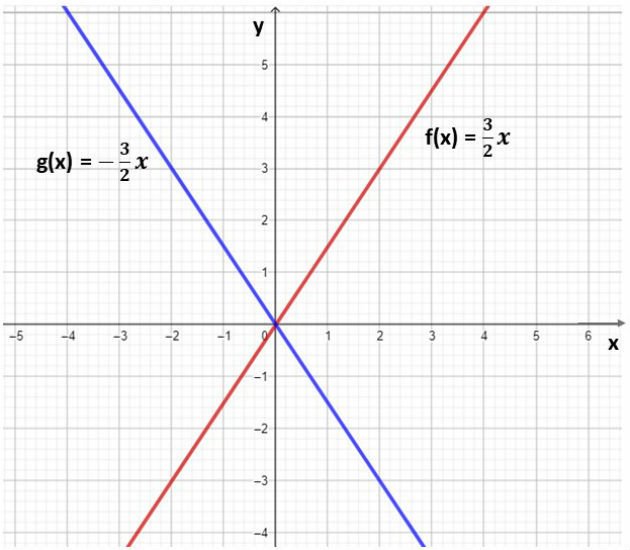
A reta da função linear é a bissetriz entre o primeiro e o terceiro quadrantes do plano cartesiano, isso significa que a reta divide os dois quadrantes em dois ângulos iguais.

               
Fonte:https://mundoeducacao.bol.uol.com.br/matematica/funcao-linear.htm

Função constante:

É toda função escrita como f(x)=b, pois a= 0. A reta sempre será paralela ao eixo x e ela sempre passará pelo ponto (0, b).

f(x)= b

f(x)=2

               
Fonte:https://www.youtube.com/watch?v=kogxDV_Mhtw

Função linear:

É toda função escrita com b=0 e a≠0. O gráfico desta função é inclinado em relação ao eixo x e sempre passa pelo ponto (0,0).

Esta função tem a seguinte lei de formação:

y=ax

Exemplos
f(x)= -3x

f(x)= 2x

                
Fonte:https://mundoeducacao.bol.uol.com.br/matematica/funcao-linear.htm

Função crescente:

Uma função linear crescente é aquela na qual a medida que atribuímos valores maiores para  x, o da imagem aumenta também. Para verificar se uma função afim  é crescente, basta verificar se o coeficiente angular da função é maior que 0, ou seja, se a > 0.

Exemplo

2x - 4 é função crescente, pois a=2(a > 0)

Função decrescente:

Uma função linear decrescente é aquela na qual a medida que atribuímos valores maiores para  x, o da imagem diminui. Para verificar se uma função afim é decrescente, basta verificar se o coeficiente angular da função é menor que 0, ou seja, se a < 0.

Exemplo:
f(x)= -2x + 4 é uma função decrescente, pois a= -2 (a <  0)

Dominando o conhecimento: Exercícios:

Questão 1) Em uma determinada cidade, a tarifa cobrada pelos taxistas corresponde a uma parcela fixa chamada de bandeirada e uma parcela referente aos quilômetros rodados. Sabendo que uma pessoa pretende fazer uma viagem de 7 km em que o preço da bandeirada é R$ 4,50 e o custo por quilômetro rodado é igual a R$ 2,75, determine:

a) Uma fórmula que expresse o valor da tarifa cobrada pelos quilômetros rodados para essa cidade

b) Quanto irá pagar a pessoa referida no enunciado?

Questão 2) Cefet - MG - 2015

Um motorista de táxi cobra, para cada corrida, uma taxa fixa de  R$ 5,00 e mais R$ 2,00 por quilômetro rodado. O valor total arrecadado (R) num dia é função da quantidade total (x) de quilômetros rodados e calculado por meio da função R(x)= ax + b, em que a é o preço cobrado por quilômetros e b, a soma de todas as taxas fixas recebidas no dia.

Se, em um dia, o taxista realizou 10 corridas e arrecadou R$ 410,00, então a média de quilômetros rodados por corrida, foi de:

a) 14

b) 16

c) 18

d) 20

Questão 3) Se f(x)= 3x + 2, qual o valor de x para f(x)= 5

a) 0

b) 1

c) 2

d) 3

e) 4

Questão 4) Um atleta ao ser submetido a um determinado treino específico apresenta, ao longo do tempo, ganho de massa muscular. A função P(t)= P0 + 0,19t expressa o peso do atleta em função do tempo ao realizar esse treinamento, sendo P0 o seu peso inicial e t o tempo em dias.

Considere um atleta que antes do treinamento pesava 55 kg e que necessitava chegar aos 60 kg em um mês. Fazendo unicamente esse treinamento, será possível alcançar o resultado esperado

Questão 5) Uma função é dada por f(x)=3x - 6. A raiz dessa função é:

a) 0

b) 1

c) 2

d) 3

e) 4

Resolução:

Questão 1- item a) 

I) Visto que a bandeirada não depende dos quilômetros, temos que b=4,5.

II) Como cada quilômetro rodado deve ser multiplicado por 2,75. Com isso, temos que este será o valor da taxa de variação, logo a= 2,75

III) Considerando p(x) como o valor da tarifa e os dados do problema, a função será escrita na seguinte forma:

                

 p(x)= 2,75x + 4,5

Resposta:  p(x)= 2,75x + 4,5

Questão 1-item b)

I) Agora que conhecemos a função, basta substituir x por 7.

  p(x)= 2,75x + 4,5

  p= 2,75 • 7 + 4,5

  p=19,25 + 4,50

  p=23,75

Resposta:A pessoa pagará R$ 23,75 por uma viagem de 7 km.

Questão 2)

I) Visto que b depende do produto da taxa fixa com o número de corridas, temos que b= 5 • 10= 50

II) Como cada quilômetro rodado deve ser multiplicado por 2. Com isso, temos que este será o valor da taxa de variação, logo a= 2

III) Considerando R(x) como o valor arrecado pelo táxi e os dados do problema, a função será escrita na seguinte forma:

R(x)=2x + 50

IV) Visto que o valor arrecadado pelo táxi (R= 410) e os dados do problema, os quilômetros rodados pelo taxista será encontrado pela seguinte equação:

      2x + 50= 410

      2x= 410 - 50

      2x= 360

        x= 360 

               2

           x=180 km

V) Como o taxista fez dez corridas, a média de quilômetros rodados por corrida será:

        y= 180 

              10

         y=18 km/corrida

Resposta: Item c.

Questão 3) Para encontrarmos o valor de x para o qual f(x)=5, basta desenvolvermos a seguinte equação

       

          f(x)=3x+2

         5= 3x +2

          3x + 2=5

          3x= 5 - 2

          3x= 3

            x= 3 

                 3

             x=1

Resposta: Item b.

Questão 4)

I) Substituindo o tempo indicado na função,  podemos encontrar o peso final do atleta e verificar se ele consegue alcançar sua meta.

 Para que o problema seja resolvido, basta substituir P0 por 55 e t por 30 na expressão, pois seu valor deve ser dado em dias:

                P(t)= P0 + 0,19t

                P(30)= 55 + 0,19 • 30

                P(30)=55+ 5,7

                P(30)=60,7 kg

Resposta: O atleta terá 60,7 kg ao final de 30 dias. Logo, é possível para o atleta alcançar a sua meta fazendo unicamente este tratamento.

Questão 5) 

I) Como encontrar a raiz de uma função significa encontrar o valor para o qual f(x)=0, teremos a seguinte equação:

             3x - 6= 0

             3x= 0 + 6

             3x= 6

               x= 6 

                    3

                x=2

Resposta: Item c.

             

Agradecimentos:

Agradeço a todos que prestigiaram meu blog e espero que gostem das atuais e futuras postagens do blog. Quem tiver dúvidas, pode comentá-las. Espero ter ajudado.

Referências:

1-https://escolakids.uol.com.br/funcao-afim.htm

2-https://www.infoescola.com/matematica/funcao-afim/

3-https://www.todamateria.com.br/funcao-afim/

4-https://www.stoodi.com.br/blog/2018/06/13/funcao-afim/

5-https://www.somatematica.com.br/emedio/funcao1/funcao1.php
6-https://mundoeducacao.bol.uol.com.br/matematica/funcao-linear.htm
7-https://www.youtube.com/watch?v=kogxDV_Mhtw
8-https://blog.maxieduca.com.br/tipos-funcao-plinomial/imagem-5-2/