Definições básicas de seno, cosseno e tangente

Introdução:

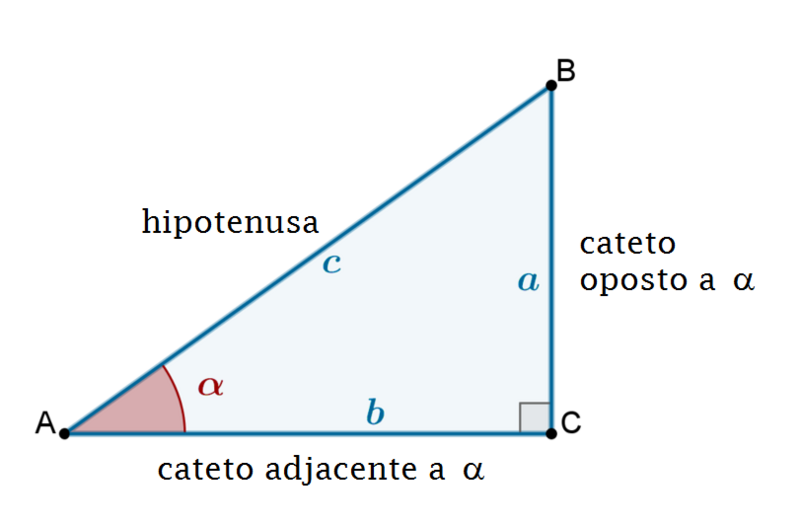
Seno, cosseno e tangente de um ângulo são relações trigonométricas obtidas a partir das razões entre os lados de um triângulo retângulo. Vale mencionar que triângulos retângulos são aqueles cujo um dos ângulos internos vale 90°. O seu maior lado é conhecido como hipotenusa e os outros dois como catetos.


Fonte:https://wikiciencias.casadasciencias.org/wiki/index.php/Ficheiro:RelacTrig1.png

Definições:

Dado um triângulo retângulo e definimos um  dos dois ângulos agudos como sendo α, obtém-se que:

sen α= cateto oposto a α =  a  
               hipotenusa            c

cos α= cateto adjacente a α =   b  
                 hipotenusa               c

tg α=    cateto oposto a α       =   a  
           cateto adjacente a α         b 

-Macete 1: O seno é sempre a razão entre o lado "separado" do ângulo e a hipotenusa, enquanto o cosseno é sempre a razão entre o lado "colado" ao ângulo e a hipotenusa.

-Macete 2: Soh Cah Toa
Soh significa seno igual oposto sobre hipotenusa
Cah significa cosseno igual adjacente sobre hipotenusa
Toa significa tangente igual oposto sobre adjacente

Exemplos: Considerando o triângulo retângulo abaixo, calcule:

-Seno de α

sen α=  cateto oposto a α = 3/5

                 hipotenusa       

sen α= 0,6

-Cosseno de α

cos α=  cateto adjacente a α = 4/5

                  hipotenusa

cos α= 0,8

-Tangente de α

tg α=     cateto oposto a α       = 3/4

            cateto adjacente a α  

tg α= 0,75

Valores de Seno, Cosseno e tangente:

Os valores de seno, cosseno e tangente são números reais que variam de valor de acordo com a variação do ângulo α. Dois triângulos retângulos que apresentam  ângulos α de mesma medida são semelhantes e, portanto, as medidas destas razões trigonométricas são iguais e os segmentos destas figuras proporcionais.

Ou seja, não importa o quão grandes ou pequenas sejam as medidas dos lados de um triângulo retângulo cujo um dos ângulos mede 30°, pois o seno deste ângulo sempre medirá 1/2 pois em um triângulo retângulo cujo um dos ângulos mede 30°, a medida da hipotenusa sempre será o dobro da medida do lado oposto a esse ângulo.

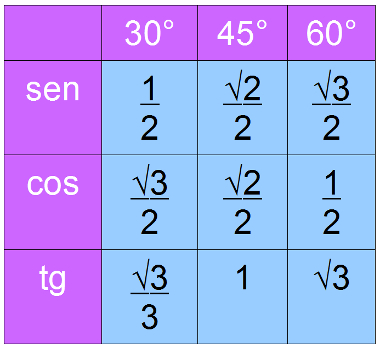
A tabela abaixo apresenta valores de seno, cosseno e tangente dos ângulos notáveis, que são 30°, 45° e 60°.

Macete- Lembre-se desta canção:“um, dois, três. Três, dois, um. Tudo sobre dois, só não tem raiz o um!”

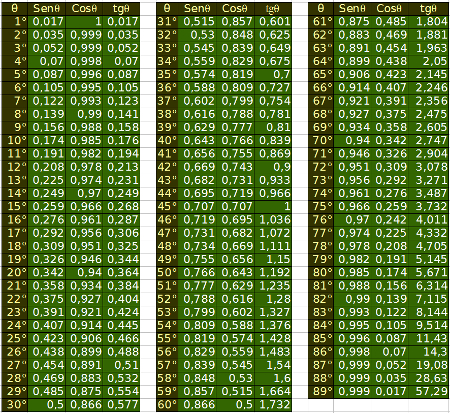
Estes valores podem ser encontrados através de cálculos nos quais as medidas dos lados e dos ângulos internos do triângulo são conhecidos. Tais valores,  são encontradas na tabela abaixo:

Fonte:https://mundoeducacao.bol.uol.com.br/matematica/tabelas-razoes-trigonometricas.htm

Agradecimentos:

Agradeço a todos que prestigiaram o meu blog e espero que gostem das atuais e futuras postagens. Quem tiver dúvidas, pode comentá-las. Espero ter ajudado.

Referências:

1-https://matika.com.br/trigonometria-no-triangulo-retangulo/definicoes-basicas---seno-cosseno-e-tangente

2-https://brasilescola.uol.com.br/o-que-e/matematica/o-que-sao-seno-cosseno-tangente.htm

3-https://mundoeducacao.bol.uol.com.br/matematica/seno-cosseno-tangente.htm

4-https://matematicabasica.net/seno-cosseno-e-tangente/

5-https://wikiciencias.casadasciencias.org/wiki/index.php/Ficheiro:RelacTrig1.png

6-https://vemqueteexplico.blogspot.com/2013/09/terno-pitagorico.html

7-http://matematicaeumaciencia.blogspot.com/2014/05/soh-cah-toa-uma-maneira-de-lembrar-como.html

Desafios de matemática 4.0

Questão 1) ITA
Os catetos b e c de um triângulo retângulo de altura h (relativa à hipotenusa) são dados pelas seguintes expressões: b = √︂( k + 1/k) e c = √︂( k − 1/k) onde k é um número real maior que 1. Calcule o valor de h em função de k.

Questão 2) (C.N)
O aluno Mauro, da a 8 série de um certo colégio, para resolver a equação x⁴ - x² + 2x - 1=0, no conjunto dos números reais, observou que  x⁴= x² - 2x + 1  e que o segundo membro da equação é um produto notável. Desse modo, concluiu que é igual a (2x + 1)²:
a) 3
b) 4
c) 5
d) 6
e) 7

Questão 3) (EUA) Se r² – r –10= 0, então (r + 1)(r + 2)(r –4) é:
a) Inteiro
b) Positivo e irracional
c) Negativo e irracional
d) Racional e não inteiro
e) Não real

Questão 4) (OBM – 2002) Se xy = 2 e x² + y²= 5, então x²/y² + y²/x² + 2 é:
a) 5/2
b) 25/4
c) 5/4
d) 1/2
e) 1

Questão 5) (OMPARA) A soma √(6 + 4√2) - √(6- 4√2) é igual a:
a) 1
b) 2
c) 3
d) 4
e) 5

Resoluções:

Questão 1) (ITA)

I) Primeiramente, será determinada a hipotenusa deste triângulo retângulo a partir do Teorema de Pitágoras

a²= b² + c²

a²= k + 1/k + k - 1/k= 2k

a=√2k

II) Agora, a relação métrica a • h= b • c, determina-se que a altura do triângulo retângulo em função de k será:

a • h= b • c
√2k • h= √︂( k + 1/k) • √︂( k - 1/k)
√2k • h= √︂( k² + 1/k²)=√︂[(k⁴ - 1)/k²]
h= √︂[(k⁴ - 1)/k² •2k]
h=√︂[(k⁴ - 1)/2k³]

Questão 2) (C.N)
I) Fatorando o segundo membro da equação, obtém-se:
x⁴= x² - 2x + 1
x⁴= (x - 1)²
x⁴ - (x - 1)²= 0

II) A partir disso, obtém-se uma diferença de quadrados que resultará em duas equações quadráticas:
(x²)² - (x - 1)²= 0
(x² + x - 1) (x² - x + 1)= 0

III) Resolvendo x² + x - 1= 0 através da fórmula resolutiva (Bhaskara)
∆= b² - 4ac= 1² - 4 • 1 • (-1)
∆= 1 + 4= 5 (a equação apresenta raízes reais diferentes)

x= -1 ± √5 =  -1 ± √5 
       2 • 1            2
x'= -1 + √5 
           2
x"=  -1 - √5  
            2
IV) Resolvendo x² - x + 1= 0 através da fórmula resolutiva (Bhaskara)
∆= b² - 4ac= (-1)² - 4 • 1 • (1)
∆= 1 - 4= -3 (esta equação não apresenta raízes reais)

V) Conjunto solução nos reais é S={(-1 ± √5)/2}. Substituindo estes valores, conclui-se que 
(2x + 1)²= 5

Resposta: Item c

Questão 3) (EUA)
I) Primeiramente, deve-se resolver a equação quadrática dada. Para isso, aplicaremos a fórmula de Bhaskara.
r² – r –10= 0
∆= b² - 4ac= 1² - 4 • 1 • (-10)
∆= 1 + 40= 41 (a equação apresenta raízes reais diferentes)


r= -1 ± √41 =  -1 ± √41 
       2 • 1              2 
*É possível observar que √41 é irracional e, por isso,utilizaremos √41≅ 6,4. Com isso, teremos:
r'≅ (-1 + 6,4)/2≅ 2,7
r"≅ (-1 - 6,4)/2≅ -3,7

III) Por fim, observe que ao utilizar a primeira solução na expressão (r + 1)(r + 2)(r –4), o valor de 
(r -4) ficará negativo e os demais termos serão positivos. Com isso, teremos um valor irracional e negativo para a express;ao.
Ao substituir a segunda solução na expressão (r + 1)(r + 2)(r –4), todos os termos da expressão são negativos e irracionais, assim como o valor da expressão. Assim, a resposta será o item c.

Resposta: Item c

Questão 4)
I) Igualando o denominador em todos os termos da expressão, obtém-se

x²/y² + y²/x² + 2= (x⁴ + 2x²y² + y⁴)/x²y²

II) Fatorando a expressão e utilizando x² + y²= 5 e xy=2, conclui-se que:

x²/y² + y²/x² + 2= (x⁴ + 2x²y² + y⁴)/x²y²=
= (x² + y²)²/(xy)²= 5²/2²
x²/y² + y²/x² + 2= 25/4

Resposta: Item b

Questão 5) (OMPARA)

I) Primeiramente, chamaremos o valor da soma de x para elevarmos ao quadrado ambos os lados da expressão e, então, aplicaremos os conceitos de produtos notáveis. Para facilitar os cálculos chamaremos 6 + 4√2de a e 6 - 4√2 de b. Reescrevendo a equação, teremos:

x= √a + √b

x²=  (√a + √b)²

x²= a + 2 • √a • √b + b

x²= a + b + 2 √ab

II) Agora, iremos reinserir o valor de a e b para determinar o valor de x.

x²= a + b + 2 √ab

x²=  6 + 4√2 +  6 - 4√2 + 2 • √[( 6 + 4√2) • ( 6 - 4√2)]

x²= 12 + 2• √[6² - (4√2)²]

x²= 12 +  2• √[36 - 32]

x²= 12 + 2 • √4

x²= 12 + 2 • 2
x²= 12 + 4
x²= 16
x= √16
x= 4

Resposta: Item d

Teorema de Tales

Construindo o conhecimento:

Tales de Mileto foi um importante filósofo, matemático e astrônomo do período pré-socrático que viveu em meados de 650 A.C. Quando tentou calcular a altura de uma pirâmide (sem uma régua ou uma trena), desenvolveu um teorema no qual afirma que:"Num plano, a interseção entre duas retas paralelas e transversais forma segmentos de reta proporcionais". Veja:

      
Fonte:https://www.todamateria.com.br/teorema-de-tales/

Exemplo: Determine o valor de x na figura abaixo.

Pela definição do Teorema de Tales, obtemos:

  (4x + 8)  =  (4x + 20) 

  (4x - 8)             4x

Desenvolvendo a expressão:

4x • (4x + 8)= (4x - 8) • (4x + 20)
16x² + 32x= 16x² + 80x - 32x -160
16x² + 32x= 16x² + 48x - 160
16x² - 16x² + 32x - 48x= -160
-16x= -160 ⇒ x= 10

Resposta: x=10

Aplicações no dia a dia:

Este teorema é muito prático na determinação de medidas através da proporcionalidade. Por isso, ele é utilizado na medição de distâncias inacessíveis e, consequentemente, possui grande aplicabilidade na astronomia e suas questões. Além disso, ele é essencial para problemas que envolvem semelhança de triângulos.

Dominando o conhecimento - exercícios:

Questão 1) (UFSM - 03) A crise energética tem levado as médias e grandes empresas a buscarem alternativas na geração de energia elétrica para a manutenção do maquinário. Uma alternativa encontrada por uma fábrica foi a de construir uma pequena hidrelétrica, aproveitando a correnteza de um rio que passa próximo às suas instalações. Observando a figura e admitindo que as linhas retas r, s e t sejam paralelas, pode-se afirmar que a barreira mede, em metros:

            

Fonte:https://exercicios.mundoeducacao.bol.uol.com.br/exercicios-matematica/exercicios-sobre-teorema-tales.htm

a) 33

b) 38

c) 43

d) 48

e) 53

Questão 2) (FUVEST-SP) Três terrenos têm frente para a rua A e para a rua B, como na figura. As divisas laterais são perpendiculares à rua A. Qual a medida de frente para a rua B de cada lote, sabendo que a frente total para essa rua tem 180 m?

Fonte:https://brasilescola.uol.com.br/matematica/teorema-tales.htm

Questão 3) (CEFET/MG-2014) Considere a figura em que r//s//t

Fonte:https://www.todamateria.com.br/teorema-de-tales-exercicios/

O valor de x é:

a) 3

b) 4

c) 5

d) 6

Questão 4)(Enem - 2009)- A rampa de um hospital tem na sua parte mais elevada uma altura de 2,2 metros. Um paciente ao caminhar sobre a rampa percebe que se deslocou 3,2 metros e alcançou uma altura de 0,8 metros. A distância em metros que o paciente ainda deve caminhar para atingir o ponto mais alto da rampa é:
a) 1,16 metros
b) 3,0 metros
c) 5,4 metros
d) 5,6 metros
e) 7,04 metros

Resoluções:

Questão 1) 

I) Considerando x como a medida da barreira e aplicando o teorema de Tales, obteremos:

 (x + 30 + 2) =  56  =  7  
         30            24      3
II) Desenvolvendo esta expressão:
3(x + 32)= 30 • 7
3x + 96= 210
3x= 210 - 96
3x= 114
x= 114/3
x= 38 metros

Resposta: Item b.


Questão 2)
I) Escrevendo as medidas dos lotes como x, y, z e aplicando o Teorema de Tales.
- Medida da rua B= x + y + z= 180 m


  x  =  y  =  z  =     x + y + z     =  180  = 2
 40    30    20     40 + 30 + 20       90

II) A partir do valor desta proporção, descobre-se x, y, z.

  x  = 2 ⇒  x= 80 m
 40

  y  = 2 ⇒  y= 60 m
 30

   z   = 2 ⇒  z= 40 m
  20

Resposta: As medidas da frente dos lotes em relação à rua B são: 80, 60 e 40 metros.

Questão 3)

I) Para encontrar o valor de x, aplicaremos o Teorema de Tales. Com isso, teremos a seguinte proporção:

  (x + 2)  =  (2x + 7)  
       x           (x + 6)

Desenvolvendo com a multiplicação cruzada:

(x + 2) • (x + 6)= x • (2x +7)
x² + 8x + 12= 2x² + 7x
2x² + 7x= x² + 8x + 12
2x² - x² + 7x - 8x - 12= 0
x² - x - 12= 0

II) Resolvendo a equação do segundo grau através da fórmula de Bháskara.
∆=b² - 4ac
∆=(-1)² - 4 • 1 • (-12)
∆= 1 + 48
∆= 49

x=  1 ± √49 
          2
x=  1 ± 7 
         2

x'=  1 + 7  =  8  
          2         2
x'= 4

x"=  1 - 7  = -  6  
           2           2
x"= -3 (não serve, por ser uma medida de segmento)

Resposta: Item b. x= 4

Questão 4)
I) A rampa descrita na questão tem suas medidas representadas na seguinte figura:

Fonte:https://www.infoenem.com.br/garanta-as-melhores-apostilas-para-o-enem-2014/

II) A partir da figura e do Teorema de Tales, obtém-se a seguinte proporção:

  (x + 3,2)  =  2,2  
       3,2          0,8

Desenvolvendo:

0,8 • (x + 3,2)= 3,2 • 2,2
0,8x + 2,56= 7,04
0,8x= 7,04 - 2,56
0,8x= 4,48
x= 4,48/0,8
x= 5,6 metros

Resposta: Item d. x= 5,6 metros.

Agradecimentos:

Agradeço a todos que prestigiaram o meu blog e espero que gostem das atuais e futuras postagens.
Quem tiver dúvidas, pode comentá-las. Espero ter ajudado.

Referências:

1-https://www.todamateria.com.br/teorema-de-tales/

2-https://brasilescola.uol.com.br/matematica/teorema-tales.htm

3-https://mundoeducacao.bol.uol.com.br/matematica/teorema-tales.htm

4-https://www.infoescola.com/matematica/teorema-de-tales/

5-https://exercicios.mundoeducacao.bol.uol.com.br/exercicios-matematica/exercicios-sobre-teorema-tales.htm

6-https://exercicios.brasilescola.uol.com.br/exercicios-matematica/exercicios-sobre-teorema-tales.htm
7-https://www.infoenem.com.br/garanta-as-melhores-apostilas-para-o-enem-2014/
8-

Desafios de matemática 3.0

Desafio 1-(ITA) Num triângulo acutângulo ABC, o lado oposto ao ângulo  mede 5 cm. Sabendo que Â= arccos 3/5 e C = arcsen 2/√5 , então a área do triângulo ABC é igual a:
a) 5/2 cm²
b) 12 cm²
c) 15 cm²
d) 2√5 cm²
e)  25/2 cm²

Resolução:
I) Primeiramente, sabemos que:
Â= arccos 3/5 => cos Â= 3/5
C = arcsen 2/√5 => sen C= 2/√5

* Agora, aplicaremos a relação fundamental da trigonometria para descobrir sen  e cos C. Ambos serão importantes para a resolução da questão posteriormente.
-sen Â
sen² Â + cos² Â= 1
sen² Â= 1 - cos² Â
sen² Â= 1 - (3/5)²
sen² Â= 1 - 9/25
sen² Â= (25 - 9)/25
sen² Â= 16/25
sen Â= √(16/25)
sen Â= 4/5

- cos C
sen² C + cos² C= 1
cos² C= 1 - sen² C
cos² C= 1 - (2/√5)²
cos² C= 1 - 4/5
cos² C= (5 - 4)/5
cos² C= 1/5
cos C= √(1/5)
cos C= 1/√5


II) Aplicando a Lei dos Senos:

      5      =       c      
  sen         sen C

c= 5 • sen C  = 5 •     1      • sen C
        sen               sen Â

c= 5 •  5   •   2  =   25   
            4      √5     2√5

Racionalizando, teremos:
c=   5√5    cm
         2
III) A área deste triângulo é dada por:

A=   1    • a • c • sen (π - A -C)
        2
Por consequência da simetria do círculo trigonométrico, sen (π - A -C)= sen (A + C).

A=   1    • a • c • sen (A + C)
        2

A=   1    • 5 •    5√5    • sen (A + C)
        2                 2

A=    25√5    • sen (A + C)
            4

sen (A + C)= sen A • cos C + sen C • cos A

sen (A + C)=   4   •   1   +    2   •   3  =    10   
                        5      √5       √5       5       5√5
sen (A + C)=   2  
                       √5

A=    25√5    •    2  
            4            √5

A=  25   cm²
        2

A= 25/2 cm²

Resposta: Item e.

Desafio 2-(ITA) Num cone circular reto, a altura é a média geométrica entre o raio da base e a geratriz. A razão entre a altura e o raio da base é:
a) (1 + √5)/2
b)(-1 + √5)/2
c)√(-1 + √5)/2
d)(-1 +  ³√5)/2
e)√[(1 + √5)/2]

Resolução:
I) De acordo com a questão, a altura é a média geométrica entre o raio da base e a geratriz. Tendo conhecimento disso e da aplicação do Teorema de Pitágoras em um cone, teremos o seguinte desenvolvimento:

- Teorema de Pitágoras em um cone circular reto:
g²= h² + R² => h² = g² - R²
h² = g² - R² (equação 1)

-Relação mencionada na questão

h= √(R • g)

- Elevando os membros desta igualdade ao quadrado, teremos:

h²=[√(R • g)]²
h²= R • g ( Equação 2)

- Substituindo a equação 1 na equação 2, teremos a seguinte igualdade:
h²= R • g
g² - R²= Rg
g² - Rg - R²= 0

II) Agora, resolveremos esta equação do segundo grau de modo a determinar o valor da geratriz do cone em função do raio de sua base.
g² - Rg - R²= 0
∆=b² - 4ac
∆= (-R)² - 4 • 1 • (-R²)
∆=R² + 4R²
∆= 5R²

g= (-b ± √∆)/2a
g= (R ± √5R²)/2
g= R[(1 ± √5)/2]
g'=R[(1 + √5)/2]
g"= R[(1 - √5)/2] (não serve, pois a geratriz não pode ter medida negativa)

III) Tendo em vista que a questão pede a razão entre a altura e o raio do cone, a resposta será:

(h/R)= [√(Rg)/R]

- Elevando os membros desta igualdade ao quadrado, teremos:

(h/R)²=[√(Rg)/R]²
(h/R)²= Rg/R²
(h/R)²= g/R
-Como a relação geratriz-raio já nos é conhecida, nós iremos utilizá-la para descobrir a resposta:
(h/R)²= R[(1 + √5)/2]/R
(h/R)²= [(1 + √5)/2]
(h/R)= √[(1 + √5)/2]

Resposta:(h/R)= Item e.

Desafio 3-(AFA) Se as dimensões, em centímetros, de um paralelepípedo reto retangular são dadas pelas raízes da equação 24x³ − 26x² + 9x − 1 = 0, então o comprimento da diagonal é igual a:
a) 7/12 cm
b) 9/24 cm
c) 24/12 cm
d)√61/12 cm
e) 73/12 cm

Resolução:
I) Primeiramente, vamos determinar quais são os coeficientes desta equação:
 24x³ − 26x² + 9x − 1 = 0

coeficientes:
a= 24
b= -26
c= 9
d= -1

II) Feito isso, iremos utilizar duas relações entre as raízes desta equação cúbica.]
Raízes da equação => r, s, t
* Soma das raízes- primeira relação

r + s + t= -b/a
r + s + t= -(-26)/24
r + s + t= 26/24
r + s + t= 13/12

* Segunda relação

r • s + s • t + r • t= c/a
r • s + s • t + r • t= 9/24
r • s + s • t + r • t= 3/8

III) Sabendo a fórmula da diagonal de um paralelepípedo e as duas relações entre as raízes da equação mencionadas anteriormente, encontraremos a resposta.

-Diagonal do paralelepípedo
d²= r² + s² + t²

* Agora, adicionaremos 2(x' • x" + x" • x''' + x' • x"') nos dois membros da equação para facilitar os cálculos.

d²  + 2 (r • s + s • t + r • t)= r² + s² + t² + 2 (r • s + s • t + r • t')
d²  + 2 (r • s + s • t + r • t)= (r + s + t)²
d² + 2 • (3/8)= (13/12)²
d² + 3/4= 169/144

* Multiplicando ambos os lados da equação por 144

144 • (d² + 3/4)= (169/144) • 144
144d² + 108= 169
144d²= 169 - 108
144d²= 61
d²= 61/144 => d=√61/12

Resposta: Item d



Referências:
1-http://ganuff.weebly.com/uploads/1/9/2/5/19255685/polinmios_e_relaes_de_girard.pdf
2-https://rumoaoita.com/wp-content/uploads/2017/03/geometria_plana_geometria_plana_no_vestibular_do_ita_ita.pdf
3-http://projetomedicina.com.br/site/attachments/article/412/matematica_geometria_espacial_cones_exercicios.pdf
4- http://pir2.forumeiros.com/t52709-afa-2000

Racionalização de denominadores

Introdução:

A racionalização de denominadores é um processo utilizado para tornar um denominador irracional em um denominador racional. Esta técnica é utilizada porque o resultado da divisão por um número irracional apresenta um valor pouco preciso.
Lembrando-se de que quando multiplicamos o numerador e denominador de uma fração por um mesmo valor, teremos uma fração equivalente, ou seja, frações que representam o mesmo valor.
A racionalização de denominadores segue o mesmo princípio, só que o número escolhido para multiplicar o denominador e numerador da fração em questão é chamado de conjugado, ou racionalizante. Portanto, a racionalização de denominadores consiste na obtenção de uma fração com denominador racional, equivalente a uma anterior com denominador irracional que possuísse um ou mais radicais.

Fator racionalizante e principais casos de racionalização:

Fator racionalizante é um número que, quando multiplicado com um número irracional, torna este último um número racional, ou seja, sem raiz.

Os principais casos de racionalização são

-Primeiro caso: O denominador é uma raiz quadrada:

   1   =   1    •    √3  =  √3  
  √3      √3        √3       √3

* O fator racionalizante de √a é √a, pois √a • √a= a

-Segundo caso: O denominador é um radical cujo índice é diferente de 2.

   2   =    2    •   3√(7)²  = 2 • 3√(7)² 

 3√7      3√7       3√(7)²          7

*O fator racionalizante de n√[(a)^m] é n√[(a)^n - m]

-Terceiro caso: O denominador é a soma, ou diferença, de dois termos.

      5      =       5        •  (3 - √3)  =  5 (3 - √3)  =   5 (3 - √3)  
 (3 + √3)    (3 + √3)      (3 - √3)        3² - (√3)²            6

* O fator racionalizante, ou conjugado, de a + √b é a - √b

A seguir, alguns outros fatores racionalizantes, de acordo com o tipo de denominador

* O fator racionalizante, ou conjugado, de √a + √b é √a - √b
* O fator racionalizante, ou conjugado, de √a - √b é √a + √b
* O fator racionalizante, ou conjugado, de √a + b é √a - b

Dominando o conhecimento:

Questão 1) CEFET/RJ-2015 Seja m a média aritmética dos números 1, 2, 3, 4 e 5. Qual é a opção que mais se aproxima do resultado da expressão abaixo?

a) 1,1

b) 1,2

c) 1,3

d) 1,4

Questão 2) IFCE 2017- Aproximando os valores de √5 e √3 até a segunda casa decimal, obtemos 2,23 e e 1,73, respectivamente. Aproximando o valor de 1/ (√5 + √3) até a segunda casa decimal, obtemos:

a) 1,98

b) 0,96

c) 3,96

d) 0,48

e) 0,25

Questão 3) Racionaliza a expressão: 1/(6 +√3)

Resoluções:

Questão 1)

I) Primeiramente, sabemos que m corresponde a média aritmética de 1, 2, 3, 4 e 5.

m= (1 + 2 + 3 + 4 + 5) 

                    5

m=   15  

          5

m= 3

II) Sabendo o valor de m, basta substituí-lo na expressão.

Resposta: Item d) 1,4.

Questão 2)

I) Primeiramente, iremos racionalizar a expressão para facilitar os cálculos.

       1         •   (√5 - √3)   =    (√5 - √3)     =  (√5 - √3)         

 (√5 + √3)      (√5 - √3)        (√5)² - (√3 )²           2

II) Agora, iremos utilizar os valores de √5 e √3 para calcular o valor aproximado desta expressão.

  (√5 - √3)   =  2,23 - 1,73  = 0,50 = 0,25

        2                      2               2

Resposta: Item e) 0,25.

Questão 3)

*Basicamente, só precisamos aplicar a racionalização de denominadores para tornar o denominador desta fração racional.

       1       =        1        •  (6 +√3) =    (6 + √3)   =    (6 +√3)  

  (6 -√3)        (6 -√3)       (6 +√3)        6² - (√3)²           3

Referências:

1-https://matematicabasica.net/racionalizacao-de-denominadores/
2-https://www.somatematica.com.br/fundam/radiciacao12.php
3-https://www.todamateria.com.br/racionalizacao-de-denominadores/
4-https://brasilescola.uol.com.br/matematica/racionalizacao-denominadores.htm
5-https://www.todamateria.com.br/radiciacao-exercicios/
6-https://files.comunidades.net/profjosecarlos/Racionalizacao_de_denominadores.pdf