Teorema de Tales

Construindo o conhecimento:

Tales de Mileto foi um importante filósofo, matemático e astrônomo do período pré-socrático que viveu em meados de 650 A.C. Quando tentou calcular a altura de uma pirâmide (sem uma régua ou uma trena), desenvolveu um teorema no qual afirma que:"Num plano, a interseção entre duas retas paralelas e transversais forma segmentos de reta proporcionais". Veja:

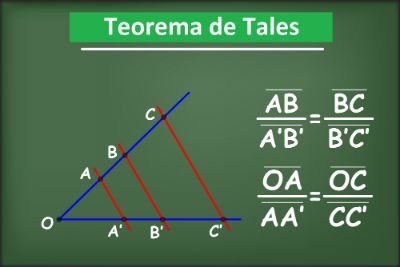
Fonte:https://www.todamateria.com.br/teorema-de-tales/

Exemplo: Determine o valor de x na figura abaixo.

Pela definição do Teorema de Tales, obtemos:

(4x + 8) = (4x + 20)

(4x - 8) 4x

Desenvolvendo a expressão:

4x • (4x + 8)= (4x - 8) • (4x + 20)
16x² + 32x= 16x² + 80x - 32x -160
16x² + 32x= 16x² + 48x - 160
16x² - 16x² + 32x - 48x= -160
-16x= -160 ⇒ x= 10

Resposta: x=10

Aplicações no dia a dia:

Este teorema é muito prático na determinação de medidas através da proporcionalidade. Por isso, ele é utilizado na medição de distâncias inacessíveis e, consequentemente, possui grande aplicabilidade na astronomia e suas questões. Além disso, ele é essencial para problemas que envolvem semelhança de triângulos.

Dominando o conhecimento - exercícios:

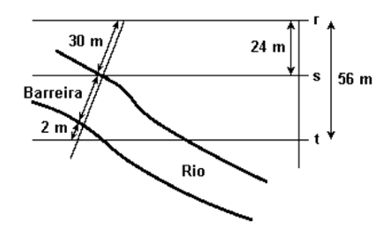
Questão 1) (UFSM - 03) A crise energética tem levado as médias e grandes empresas a buscarem alternativas na geração de energia elétrica para a manutenção do maquinário. Uma alternativa encontrada por uma fábrica foi a de construir uma pequena hidrelétrica, aproveitando a correnteza de um rio que passa próximo às suas instalações. Observando a figura e admitindo que as linhas retas r, s e t sejam paralelas, pode-se afirmar que a barreira mede, em metros:

Fonte:https://exercicios.mundoeducacao.bol.uol.com.br/exercicios-matematica/exercicios-sobre-teorema-tales.htm

a) 33

b) 38

c) 43

d) 48

e) 53

Questão 2) (FUVEST-SP) Três terrenos têm frente para a rua A e para a rua B, como na figura. As divisas laterais são perpendiculares à rua A. Qual a medida de frente para a rua B de cada lote, sabendo que a frente total para essa rua tem 180 m?

Fonte:https://brasilescola.uol.com.br/matematica/teorema-tales.htm

Questão 3) (CEFET/MG-2014) Considere a figura em que r//s//t

Fonte:https://www.todamateria.com.br/teorema-de-tales-exercicios/

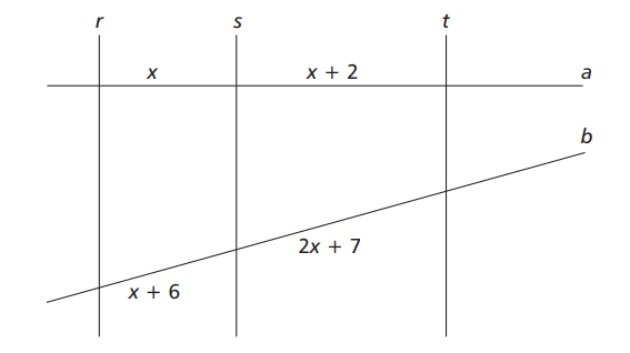
O valor de x é:

a) 3

b) 4

c) 5

d) 6

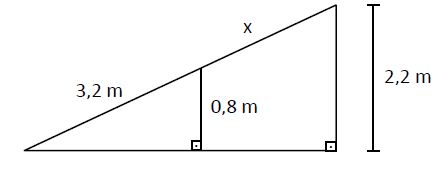
Questão 4)(Enem - 2009)- A rampa de um hospital tem na sua parte mais elevada uma altura de 2,2 metros. Um paciente ao caminhar sobre a rampa percebe que se deslocou 3,2 metros e alcançou uma altura de 0,8 metros. A distância em metros que o paciente ainda deve caminhar para atingir o ponto mais alto da rampa é:
a) 1,16 metros
b) 3,0 metros
c) 5,4 metros
d) 5,6 metros
e) 7,04 metros

Resoluções:

Questão 1)

I) Considerando x como a medida da barreira e aplicando o teorema de Tales, obteremos:

(x + 30 + 2) = 56 = 7
30 24 3
II) Desenvolvendo esta expressão:
3(x + 32)= 30 • 7
3x + 96= 210
3x= 210 - 96
3x= 114
x= 114/3
x= 38 metros

Resposta: Item b.

Questão 2)
I) Escrevendo as medidas dos lotes como x, y, z e aplicando o Teorema de Tales.
- Medida da rua B= x + y + z= 180 m

x = y = z = x + y + z = 180 = 2
40 30 20 40 + 30 + 20 90

II) A partir do valor desta proporção, descobre-se x, y, z.

x = 2 ⇒  x= 80 m
40

y = 2 ⇒  y= 60 m
30

z = 2 ⇒  z= 40 m
20

Resposta: As medidas da frente dos lotes em relação à rua B são: 80, 60 e 40 metros.

Questão 3)

I) Para encontrar o valor de x, aplicaremos o Teorema de Tales. Com isso, teremos a seguinte proporção:

(x + 2) = (2x + 7)
x (x + 6)

Desenvolvendo com a multiplicação cruzada:

(x + 2) • (x + 6)= x • (2x +7)
x² + 8x + 12= 2x² + 7x
2x² + 7x= x² + 8x + 12
2x² - x² + 7x - 8x - 12= 0
x² - x - 12= 0

II) Resolvendo a equação do segundo grau através da fórmula de Bháskara.
∆=b² - 4ac
∆=(-1)² - 4 • 1 • (-12)
∆= 1 + 48
∆= 49

x= 1 ± √49
2
x= 1 ± 7
2

x'= 1 + 7 = 8
2 2
x'= 4

x"= 1 - 7 = - 6
2 2
x"= -3 (não serve, por ser uma medida de segmento)

Resposta: Item b. x= 4

Questão 4)
I) A rampa descrita na questão tem suas medidas representadas na seguinte figura:

Fonte:https://www.infoenem.com.br/garanta-as-melhores-apostilas-para-o-enem-2014/

II) A partir da figura e do Teorema de Tales, obtém-se a seguinte proporção:

(x + 3,2) = 2,2
3,2 0,8

Desenvolvendo:

0,8 • (x + 3,2)= 3,2 • 2,2
0,8x + 2,56= 7,04
0,8x= 7,04 - 2,56
0,8x= 4,48
x= 4,48/0,8
x= 5,6 metros

Resposta: Item d. x= 5,6 metros.