Soma e subtração de arcos

Introdução:

No estudo de trigonometria, é possível reparar que a relação sen (a + b)= sen a + sen b não se prova verdadeira para quaisquer valores de a e b. Observe o exemplo abaixo:

sen 60° + sen 60°= 0,5 + 0,5= 1

Nota-se que esta relação é falsa, pois sabe-se que sen 120°= 0,5. Nem todos os valores de a e b satisfazem-na. O mesmo ocorre com estas seguintes relações abaixo:
sen (x - y)= sen x - sen y

cos (x + y)= cos x + cos y

cos (x - y)= cos x - cos y

tg (x + y)= tg x + tg y

tg (x - y)= tg x - tg y

Fórmulas de adição e subtração de arcos:

As reais fórmulas de adição e subtração de arcos são estas:

sen (a +b)= sen a • cos b + sen b • cos a
sen (a - b)= sen a • cos b - sen b • cos a
cos (a + b)= cos a • cos b - sen a • sen b
cos (a - b)= cos a • cos b + sen a • sen b

tg (a + b)= tg a + tg b

(1- tg a • tg b)

tg (a - b)=   tg a - tg b
  (1+ tg a • tg b)

Exemplo: A partir das fórmulas de adição e subtração, calcule sen 75°,cos 15° e tg 105°.
Resolução:
* sen 75°
I) Aplicando o seno da soma de dois ângulos teremos:

sen 75°= sen (45° + 30°)= sen 45° • cos 30° + sen 30° • cos 45°

sen 75°= √2   •  √3  +  1   •  √2

2 2 2 2
sen 75°= √6 + √2
4 4
sen 75°= √6 + √2
4
* cos 15°
I) Aplicando o cosseno da diferença de dois ângulos, teremos:
cos 15°= cos (45° - 30°)= cos 45° • cos 30° + sen 30° • sen 45°

cos 15°= √2 • √3 + 1 • √2

2 2 2 2

cos 15°= √6 + √2

4 4

cos 15°= √6 + √2

4
* tg 105°
I)Aplicando a tangente da soma de dois ângulos teremos:

tg 105°= tg (60° + 45°)=   tg 60° + tg 45°
(1- tg 60° • tg 45°)

tg 105°= √3 + 1
1 - √3
Racionalizando:

tg 105°= √3 + 1   •  1 + √3
  1 - √3 1 + √3

tg 105°= 2 • (2 + √3)
(-2)
tg 105°= - (2 + √3)

tg 105°= -2 - √3

Arco duplo

Se fizemos a=b nas fórmulas anteriores, teremos:

sen (a + a)= sen a • cos a + sen a • cos a

sen 2a= 2sen a • cos a

cos (a + a)= cos a • cos a - sen a • sen a
cos 2a= cos² a - sen² a

tg (a + a)=   tg a + tg a
  (1- tg a • tg a)

tg 2a= 2 tg a
1- tg² a

Exemplo: Determine cos 2a, sabendo que sen a= 1/4

I) Primeiramente, devemos lembrar que o cosseno de um arco duplo é dado por:

cos 2a= cos² a - sen² a

Escreveremos esta expressão somente em função de sen a por meio da relação fundamental da trigonometria.

sen² a + cos² a= 1

cos² a= 1 - sen² a

Substituindo a igualdade acima na fórmula do arco duplo, teremos:

cos 2a= cos² a - sen² a

cos 2a= 1 - sen² a - sen² a

cos 2a= 1 - 2 sen² a

II) Agora, determinaremos cos 2a utilizando sen a.

cos 2a= 1 - 2 sen² a

cos 2a= 1 - 2 (1/4)²

cos 2a= 1 - 2/16

cos 2a= 1 -1/8

cos 2a= 8/8 - 1/8

cos 2a= 7/8

Resposta: cos 2a= 7/8

Arco metade:

Sabe-se que cos 2a= 2cos² a - 1 e cos 2a= 1 - 2 sen² a; portanto, se fizermos 2a= x, teremos:

-cos (x/2)
cos 2a= 2cos² a - 1

cos x= 2cos² (x/2)- 1 ⇒ cos (x/2)=±√[(1 + cos x)/2]

-sen (x/2)

cos 2a= 1 - 2sen² a

cos x= 1 - 2sen² (x/2) ⇒ sen (x/2)=±√[(1 + cos x)/2]

-tg (x/2)
tg (x/2)= sen (x/2)/cos (x/2) ⇒ tg (x/2)=±√[(1 - cos x)/(1 + cos x)]

Dominando o conhecimento:

Questão 1)(PUC – SP) Se tg (x + y) = 33 e tg x = 3, então tg y é igual a:

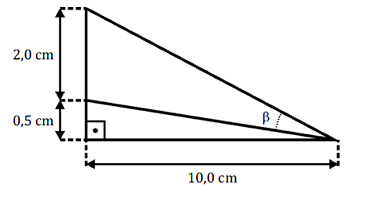
Questão 2) (Mackenzie - 2009) Na figura, tg β é igual a:

Fonte:https://www.tutorbrasil.com.br/forum/viewtopic.php?t=17098#p42613

a) 16

b) 8

c) 19

d) 2

e) 1

Questão 3) Determine o valor de A= sen 105° + cos 105°

Resoluções:

Questão 1)
I) Para se descobrir tg y, basta utilizar a fórmula da tangente da soma de dois arcos, sabendo que
tg x=3 e que tg (x + y)= 33.

tg (x + y)= tg x + tg y

(1 - tg x • tg y)

33= 3 + tg y

(1 - 3tg y)

33 • (1 - 3tg y)= 3 + tg y

33 - 99tg y= 3 + tg y

-99tg y - tg y= 3 -33

-100tg y= -30

100 tg y= 30

tg y= 30/100

tg y= 0,3

Resposta: tg y= 0,3

Questão 2)

I) Pelos dados do problema, teremos:

tg (α + β)= 2 + 0,5 = 2,5 = 1

10 10 4

tg α= 0,5 = 1

10 20

II) Aplicando a tangente da soma, teremos:

tg (α + β)= tg α + tg β

(1 - tg α • tg β)

1 + tg β

1 = 20

4 1 - tg β

1- tg β = 4 + 4tg β

20 20

Para facilitar os cálculos, multiplicaremos ambos os lados da equação por 20.

20 - tg β= 4 + 80tg β

-80tg β - tg β = 4 -20

-81tg β = -16

81tg β = 16

tg β= 16

Resposta: Item a

Questão 3)

I) Primeiramente, devemos identificar sen 105° e cos 105°. Para isso, podemos considerar
105°= 60° + 45°. Através do seno da soma de dois arcos, teremos:

sen 105°= sen (60° + 45°)
sen 105°= sen 60° • cos 45° + sen 45° • cos 60°
sen 105°= √3 • √2 + √2 • 1
2 2 2 2

sen 105°= √6 + √2

4 4

sen 105°= √6 + √2
4
A partir do cosseno da soma de dois arcos, teremos:

cos 105°= cos (60° + 45°)
cos 105°= cos 60° • cos 45° - sen 45° • sen 60°
cos 105°= 1 •   √2 -   √2 •   √3
2 2 2 2
cos 105°=   √2 -   √6
4 4
cos 105°=  √2 - √6
4

II) Agora que os valores de sen 105° e cos 105° são conhecidos, basta substituí-los na expressão:

A= sen 105° + cos 105°

A=   √6 + √2 +   √2 - √6
4 4
A=  √6 + √2 + √2 - √6
4
A=  2 √2
4

A=  √2
2

Resposta: A= √2/2.

Agradecimentos:

Agradeço a todos que prestigiaram o meu blog e espero que gostem das atuais e futuras postagens. Quem tiver dúvidas, pode comentá-las. Espero ter ajudado.

Referências:

1-https://guiadoestudante.abril.com.br/estudo/soma-e-subtracao-de-arcos-trigonometria/
2- https://educacao.uol.com.br/disciplinas/matematica/adicao-e-subtracao-de-arcos-resolucao-de-equacoes-e-inequacoes.htm
3- https://www.colegioweb.com.br/funcoes-trigonometricas-de-arco/adicao-e-subtracao-de-arcos.html
4-https://brasilescola.uol.com.br/matematica/formulas-adicao-arcos.htm
5- https://mundoeducacao.bol.uol.com.br/matematica/transformacoes-trigonometricas-formulas-adicao.htm
6-https://exercicios.brasilescola.uol.com.br/exercicios-matematica/exercicios-sobre-formulas-adicao-arcos.htm
7 -http://matematicarev.blogspot.com/2011/08/adicao-e-subtracao-de-arcos.html
8-http://nsaulasparticulares.com.br/wp-content/uploads/2014/07/Trigonometria-soma-de-arcos-sen-a-b.pdf
9-http://renataquartieri.com/wp-content/uploads/2017/04/aula-8-adicao-e-subtracao-de-arcos.pdf
10-https://www.tutorbrasil.com.br/forum/viewtopic.php?t=17098

Exatas para todos - Ensino de qualidade em quantidade

domingo, 15 de dezembro de 2019