Introdução:
Polígonos são figuras geométricas formadas por linhas fechadas, que por sua vez são constituídas por segmentos de reta que não se cruzam e que estão em um mesmo plano. Eles podem ser classificados em polígonos regulares e irregulares. Esta classificação é dada em função do tamanho dos lados e de seus ângulos. Polígonos regulares possuem ângulos e lados congruentes, enquanto os polígonos irregulares apresenta estas medidas com valores distintos.Além disso, estas figuras podem ser convexas e não convexas. Se os ângulos que formam o polígono forem menores que 180°, o polígono será regular. Caso os ângulos sejam maiores que 180°, o polígono será não convexo. Tendo estes conhecimentos em vista, abordaremos o cálculo do lado e da apótema de um polígono regular.O que é um polígono regular inscrito?
Um polígono regular inscrito em uma circunferência é aquele que se encontra dentro de uma circunferência, de modo que os seus vértices fiquem na circunferência.
É importante lembrarmos que: "todo polígono regular é inscritível em uma circunferência".
Elementos:
Todo polígono regular apresenta os seguintes elementos:
Ln=> Lado do polígono
R => Raio da circunferência inscrita em um polígono
an => medida de um apótema
n => número de lados do polígono
ac=> ângulo central do polígono
n => número de lados do polígono
ac=> ângulo central do polígono
Apótema:
A maioria dos elementos mencionados são conhecidos por muitos, mas alguns se perguntam o que é apótema.
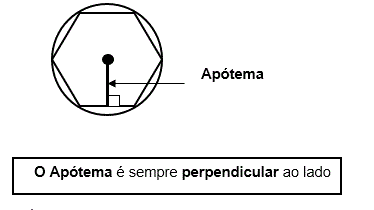
Apótema é o segmento cujas extremidades são: o centro de um polígono regular, que coincide com o centro da circunferência inscrita e circunscrita simultaneamente, e o ponto médio do seu lado.
Fórmula geral para lado de um polígono regular inscrito com número "n" de lados:
Para evitar "decorebas" de fórmulas para muitos lados e apótemas dos polígonos inscritos, demonstraremos a fórmulas generalizadas para o lado e apótema de qualquer polígono regular inscrito de "n" lados.

Fonte:http://matprofrenatas.blogspot.com/2012_03_11_archive.html
Primeiramente, devemos observar que o triângulo ∆COD é isósceles e que o seu ângulo CÔD (ac) representa o ângulo central do polígono.
Sendo CÔD= ac= 360°/ n e utilizando a Lei dos cossenos, temos que o lado de um polígono regular inscrito com número "n" de lados é dado por:
Ln²= R² + R² - 2 • R • R • cos ac
Ln²= 2R² - 2R² • cos ac
Ln²= 2R² • (1 - cos ac)
*Exemplo: determine a medida do lado de um hexágono regular inscrito em uma circunferência cujo raio mede 8 cm.
Primeiramente, devemos determinar o ângulo central do polígono em questão, sabendo que o hexágono tem seis lados. Logo, teremos:
ac= 360°/ n
ac= 360°/ 6
ac= 60°
Utilizando a fórmula geral do lado de um polígono regular inscrito temos:
Ln²= 2R² • (1 - cos ac)
L6²= 2 • 8² • (1 - cos 60°)
L6²= 2 • 64 • (1 - 0,5)
L6²= 2 • 64 • 0,5
L6²= 64
L6=√64
L6= 8 cm
-Resposta: O lado deste polígono mede 8 cm.
*Implicações desta fórmula:
Com esta fórmula podemos provar algumas relações métricas específicas do quadrado, triângulo equilátero e hexágono regular. Tais relações são:
-Relação entre lado e raio de um hexágono regular inscrito:
Primeiramente, o ângulo central do hexágono é dado por:
ac= 360°/n
ac= 360°/6
ac= 60°
Utilizando a fórmula geral do lado de um polígono regular inscrito, teremos a seguinte relação:
Ln²= 2R² • (1 - cos ac)
L6²= 2 • R² • (1 - cos 60°)
L6²= 2 • R² • (1 - 0,5)
L6²= 2 • R² • 0,5
L6²= R²
L6=√R²
L6= R
Exemplo: Determine o lado de um hexágono cujo raio mede 15 m:
-Pela relação entre o lado e o raio de um hexágono, teremos:
L6= R
L6= 15 m
Resposta: O lado deste hexágono mede 15 metros.
-Relação entre lado e raio de um quadrilátero inscrito:
Primeiramente, o ângulo central do quadrilátero é dado por:
ac= 360°/n
ac= 360°/4
ac= 90°
Utilizando a fórmula geral do lado de um polígono regular inscrito, teremos a seguinte relação:
Ln²= 2R² • (1 - cos ac)
L4²= 2 • R² • (1 - cos 90°)
L4²= 2 • R² • (1 - 0)
L4²= 2 • R² • 1
L4²= 2R²
L4=√2R²
L4= R√2
Exemplo: Determine o lado de um quadrado cujo raio mede 8 cm:
-Pela relação entre o lado e o raio de um quadrado inscrito, temos:
L4= R√2
L4= 8√2 cm
Resposta: O lado deste quadrado mede 8√2 centímetros.
-Relação entre lado e raio de um triângulo equilátero:
Primeiramente, o ângulo central do triângulo equilátero é dado por:
ac= 360°/n
ac= 360°/3
ac= 120°
Utilizando a fórmula geral do lado de um polígono regular inscrito, teremos a seguinte relação:
Ln²= 2R² • (1 - cos ac)
L3²= 2 • R² • (1 - cos 120°)
L3²= 2 • R² • (1 - (-0,5))
L3²= 2 • R² • (1 + 0,5)
L3²= 2 • R² • 1,5
L3²= 3R²
L3=√3R²
L3= R√3
Exemplo: Determine o lado de um triângulo equilátero cujo raio mede 9 cm.
-Pela relação entre o lado e o raio de um quadrado inscrito, temos:
L3= R√3
L3=9√3 cm
Resposta: O lado deste triângulo equilátero mede 9√3 centímetros.
-Fórmula para o apótema de um polígono regular inscrito com número "n" de lados:
Para demonstrar esta fórmula generalizada do apótema de um polígono regular em função do seu raio "R". Para calcular o apótema,, vamos considerar um hexágono regular cujo raio mede 6 cm.
Primeiramente, devemos observar que o triângulo ∆COD é isósceles e que o seu ângulo CÔD (ac) representa o ângulo central do polígono.
Sendo CÔD= ac= 360°/ n e utilizando a Lei dos cossenos, temos que o lado de um polígono regular inscrito com número "n" de lados é dado por:
Ln²= R² + R² - 2 • R • R • cos ac
Ln²= 2R² - 2R² • cos ac
Ln²= 2R² • (1 - cos ac)
*Exemplo: determine a medida do lado de um hexágono regular inscrito em uma circunferência cujo raio mede 8 cm.
Primeiramente, devemos determinar o ângulo central do polígono em questão, sabendo que o hexágono tem seis lados. Logo, teremos:
ac= 360°/ n
ac= 360°/ 6
ac= 60°
Utilizando a fórmula geral do lado de um polígono regular inscrito temos:
Ln²= 2R² • (1 - cos ac)
L6²= 2 • 8² • (1 - cos 60°)
L6²= 2 • 64 • (1 - 0,5)
L6²= 2 • 64 • 0,5
L6²= 64
L6=√64
L6= 8 cm
-Resposta: O lado deste polígono mede 8 cm.
*Implicações desta fórmula:
Com esta fórmula podemos provar algumas relações métricas específicas do quadrado, triângulo equilátero e hexágono regular. Tais relações são:
-Relação entre lado e raio de um hexágono regular inscrito:
Primeiramente, o ângulo central do hexágono é dado por:
ac= 360°/n
ac= 360°/6
ac= 60°
Utilizando a fórmula geral do lado de um polígono regular inscrito, teremos a seguinte relação:
Ln²= 2R² • (1 - cos ac)
L6²= 2 • R² • (1 - cos 60°)
L6²= 2 • R² • (1 - 0,5)
L6²= 2 • R² • 0,5
L6²= R²
L6=√R²
L6= R
Exemplo: Determine o lado de um hexágono cujo raio mede 15 m:
-Pela relação entre o lado e o raio de um hexágono, teremos:
L6= R
L6= 15 m
Resposta: O lado deste hexágono mede 15 metros.
-Relação entre lado e raio de um quadrilátero inscrito:
Primeiramente, o ângulo central do quadrilátero é dado por:
ac= 360°/n
ac= 360°/4
ac= 90°
Utilizando a fórmula geral do lado de um polígono regular inscrito, teremos a seguinte relação:
Ln²= 2R² • (1 - cos ac)
L4²= 2 • R² • (1 - cos 90°)
L4²= 2 • R² • (1 - 0)
L4²= 2 • R² • 1
L4²= 2R²
L4=√2R²
L4= R√2
Exemplo: Determine o lado de um quadrado cujo raio mede 8 cm:
-Pela relação entre o lado e o raio de um quadrado inscrito, temos:
L4= R√2
L4= 8√2 cm
Resposta: O lado deste quadrado mede 8√2 centímetros.
-Relação entre lado e raio de um triângulo equilátero:
Primeiramente, o ângulo central do triângulo equilátero é dado por:
ac= 360°/n
ac= 360°/3
ac= 120°
Utilizando a fórmula geral do lado de um polígono regular inscrito, teremos a seguinte relação:
Ln²= 2R² • (1 - cos ac)
L3²= 2 • R² • (1 - cos 120°)
L3²= 2 • R² • (1 - (-0,5))
L3²= 2 • R² • (1 + 0,5)
L3²= 2 • R² • 1,5
L3²= 3R²
L3=√3R²
L3= R√3
Exemplo: Determine o lado de um triângulo equilátero cujo raio mede 9 cm.
-Pela relação entre o lado e o raio de um quadrado inscrito, temos:
L3= R√3
L3=9√3 cm
Resposta: O lado deste triângulo equilátero mede 9√3 centímetros.
Para demonstrar esta fórmula generalizada do apótema de um polígono regular em função do seu raio "R". Para calcular o apótema,, vamos considerar um hexágono regular cujo raio mede 6 cm.
Fonte: https://www.oblogdomestre.com.br/2015/12/inscritoOucircunscrito.Matematica.html
Primeiramente devemos saber qual o ângulo no ponto de sai o apótema. Para isso basta determinar o ângulo central deste polígono, que é igual a 60°. Como o apótema divide o ângulo em dois outros ângulos de mesma medida,nesse caso, o ângulo mede 30°. Agora, poderemos utilizar algumas relações trigonométricas para determinar o apótema deste hexágono:
cos 30°= a
R
R • cos 30°= a
a= R • cos 30°
Sendo R= 6 cm, teremos:
a= R • cos 30°
a= 6 • cos 30°
a= 6 • √3
2
a= 2√3 cm
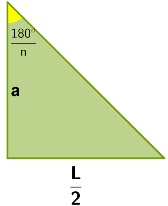
Generalizando o caso para um polígono regular de lado L, apótema a. O ângulo do apótema, ou ângulo central, é dado por 360°/ n. Como devemos dividir este ângulo por dois para aplicar trigonometria, teremos:
360°
a'= n = 360° • 1
2 n 2
a'= 180 °
n
Considerando novamente o raio "R" da circunferência inscrita como hipotenusa deste triângulo retângulo e utilizando algumas relações trigonométricas, teremos:
Fonte:https://www.infoescola.com/matematica/area-de-poligonos-regulares/
cos (180°/n)= an
R
an= R • cos (180°/n)
Primeiramente devemos saber qual o ângulo no ponto de sai o apótema. Para isso basta determinar o ângulo central deste polígono, que é igual a 60°. Como o apótema divide o ângulo em dois outros ângulos de mesma medida,nesse caso, o ângulo mede 30°. Agora, poderemos utilizar algumas relações trigonométricas para determinar o apótema deste hexágono:
cos 30°= a
R
R • cos 30°= a
a= R • cos 30°
Sendo R= 6 cm, teremos:
a= R • cos 30°
a= 6 • cos 30°
a= 6 • √3
2
a= 2√3 cm
Generalizando o caso para um polígono regular de lado L, apótema a. O ângulo do apótema, ou ângulo central, é dado por 360°/ n. Como devemos dividir este ângulo por dois para aplicar trigonometria, teremos:
360°
a'= n = 360° • 1
2 n 2
a'= 180 °
n
Considerando novamente o raio "R" da circunferência inscrita como hipotenusa deste triângulo retângulo e utilizando algumas relações trigonométricas, teremos:

Fonte:https://www.infoescola.com/matematica/area-de-poligonos-regulares/
cos (180°/n)= an
R
an= R • cos (180°/n)
Exemplo: Determine o apótema de um triângulo equilátero inscrito cujo raio mede 40 cm.
Utilizando as informações fornecidas e sabendo que o triângulo equilátero tem 3 lados, teremos:
an= R • cos (180°/n)
a3= 40 • cos (180°/3)
an= 40 • cos 60°
a3= 40 • 0,5
a3= 20 cm
*Implicações desta fórmula:
Assim como a fórmula geral do lado de um polígono regular, esta fórmula geral do apótema nos permite desenvolver relações métricas simples do triângulo equilátero, quadrado e hexágono. Tais relações são:
Apótema de um hexágono regular:
* Sabendo que um hexágono apresenta seis lados, teremos a seguinte relação:
an= R • cos (180°/n)
a6= R • cos (180°/6)
a6= R • cos 30°
a6= R • √3
2
a6= R√3
2
*Exemplo: Determine a apótema de um hexágono inscrito cujo raio mede 14 cm.
-Pela relação entre o raio de um quadrado inscrito e o seu apótema, teremos:
R= 14 cm
a6= R√3
2
a6= 14√3
2
a6= 7√3 cm
Resposta: O apótema deste hexágono mede 7√3 cm.
Apótema de um quadrado:
* Sabendo que um quadrado apresenta quatro lados, temos a seguinte relação:
an= R • cos (180°/n)
a4= R • cos (180°/4)
a4= R • cos 45°
a4= R • √2
2
a4= R√2
2
*Exemplo: Determine a apótema de um quadrado inscrito cujo raio mede 20 cm.
-Pela relação entre o raio de um quadrado inscrito e o seu apótema, teremos:
R= 20 cm
a4= R√2
2
a4= 20√2
2
a4= 10√2 cm
Resposta: O apótema deste quadrado mede 10√2 cm.
Apótema de um triângulo equilátero:
* Sabendo que um triângulo equilátero apresenta três lados, teremos:
an= R • cos (180°/n)
a3= R • cos (180°/3)
a3= R • cos 60°
a3= R • 1
2
a3= R/2
Exemplo: Determine o lado de um triângulo equilátero inscrito em uma circunferência cujo raio mede 10 cm.
-Pela relação entre o raio de um triângulo equilátero inscrito e o seu apótema, teremos:
a3= R/2
a3= 10/2
a3= 5 cm
Resposta: O apótema deste triângulo equilátero regular mede 5 cm.
Assim como a fórmula geral do lado de um polígono regular, esta fórmula geral do apótema nos permite desenvolver relações métricas simples do triângulo equilátero, quadrado e hexágono. Tais relações são:
Apótema de um hexágono regular:
* Sabendo que um hexágono apresenta seis lados, teremos a seguinte relação:
an= R • cos (180°/n)
a6= R • cos (180°/6)
a6= R • cos 30°
a6= R • √3
2
a6= R√3
2
*Exemplo: Determine a apótema de um hexágono inscrito cujo raio mede 14 cm.
-Pela relação entre o raio de um quadrado inscrito e o seu apótema, teremos:
R= 14 cm
a6= R√3
2
a6= 14√3
2
a6= 7√3 cm
Resposta: O apótema deste hexágono mede 7√3 cm.
Apótema de um quadrado:
* Sabendo que um quadrado apresenta quatro lados, temos a seguinte relação:
an= R • cos (180°/n)
a4= R • cos (180°/4)
a4= R • cos 45°
a4= R • √2
2
a4= R√2
2
*Exemplo: Determine a apótema de um quadrado inscrito cujo raio mede 20 cm.
-Pela relação entre o raio de um quadrado inscrito e o seu apótema, teremos:
R= 20 cm
a4= R√2
2
a4= 20√2
2
a4= 10√2 cm
Resposta: O apótema deste quadrado mede 10√2 cm.
Apótema de um triângulo equilátero:
* Sabendo que um triângulo equilátero apresenta três lados, teremos:
an= R • cos (180°/n)
a3= R • cos (180°/3)
a3= R • cos 60°
a3= R • 1
2
a3= R/2
Exemplo: Determine o lado de um triângulo equilátero inscrito em uma circunferência cujo raio mede 10 cm.
-Pela relação entre o raio de um triângulo equilátero inscrito e o seu apótema, teremos:
a3= R/2
a3= 10/2
a3= 5 cm
Resposta: O apótema deste triângulo equilátero regular mede 5 cm.
Dominando o conhecimento - exercícios:
Questão 1) Calcule com aproximação de uma casa decimal a medida do lado do decágono regular inscrita em uma circunferência cujo raio mede 6 cm. (Use cos 36°= 0,81)
Questão 2) O apótema de um hexágono regular mede 5√3 cm. Determine o perímetro do hexágono.
Questão 3) Calcule as medidas do lado e do apótema de um hexágono regular inscrito em uma circunferência cujo raio mede 12 cm.
Questão 4) Calcule a medida do lado e do apótema de um triângulo equilátero inscrito cujo raio mede 10 cm.
Questão 5) O perímetro de um hexágono regular inscrito em um círculo de 25π cm² de área é igual a:
a) 150 cm
b) 75 cm
c) 25 cm
d) 15 cm
e) 30 cm
Questão 5) O perímetro de um hexágono regular inscrito em um círculo de 25π cm² de área é igual a:
a) 150 cm
b) 75 cm
c) 25 cm
d) 15 cm
e) 30 cm
Resoluções:
Questão 1)
Primeiramente, devemos determinar o ângulo central do polígono em questão, sabendo que o decágono tem dez lados. Logo:
ac= 360°/ 10
ac= 360°/ 10
ac= 36°
Utilizando a fórmula geral do lado de um polígono regular inscrito temos:
Ln²= 2R² • (1 - cos ac)
L10²= 2 • 6² • (1 - cos 36°)
L10²= 2 • 36 • (1 - 0,81)
L10²= 2 • 64 • 0,19
L10²= 13,68
L10=√13,68
L10= 3,7 cm
Questão 2)
I) Sabendo que o apótema deste hexágono mede 5√3 cm e que o hexágono regular apresenta 6 lados, devemos determinar a medida do raio de um polígono deste por meio da fórmula geral do apótema.
a6= R • cos (180°/n)
5√3= R • cos (180°/6)
5√3= R • cos (180°/6)
5√3= R • cos 30°
5√3= R√3
2
R√3= 5√3 • 2
R√3= 10√3
R= 10 cm
II) Utilizando a fórmula geral do lado de um polígono regular inscrito, teremos:
Ln²= 2R² • (1 - cos ac)
L6²= 2 • 10² • (1 - cos 60°)
L6²= 2 • 10² • (1 - 0,5)
L6²= 2 • 10² • 0,5
L6²= 10²
L6=√10²
L6= 10 cm
III) Agora que a medida do lado deste polígono é conhecida, teremos:
2p= 10 • 6
2p= 60 cm
Resposta: 2p= 60 cm
Questão 3)
I) Primeiramente, devemos determinar o ângulo central do polígono em questão, sabendo que o hexágono tem dez lados. Logo, teremos:
ac= 360°/ 6
ac= 360°/ 6
ac= 60°
Utilizando a fórmula geral do lado de um polígono regular inscrito e sabendo que o R= 12 cm, teremos:
Ln²= 2R² • (1 - cos ac)
L6²= 2 • 12² • (1 - cos 60°)
L6²= 2 • 144 • (1 - 0,5)
L6²= 2 • 144 • 0,5= 144
L6²= 144
L6=√144
L6= 12 cm
II) A apótema será dada por:
a6= R • cos (180°/n)
a6= 12 • cos (180°/6)
a6= 12 • cos 30°
a6= 12√3
2
a6=6√3 cm
Resposta: L= 12 cm e a= 6√3 cm
Questão 4)
Primeiramente, devemos determinar o ângulo central do polígono em questão, sabendo que o triângulo equilátero tem três lados e o raio da sua circunferência inscrita mede 8 cm. Logo, teremos:
ac= 360°/ 3
ac= 360°/ 3
ac= 120°
Utilizando a fórmula geral do lado de um polígono regular inscrito e relembrando que R= 8 cm, teremos:
Ln²= 2R^2 • (1 - cos ac)
L3²= 2 • 8^2 • (1 - cos 120°)
L3²= 2 • 64 • (1 - (-0,5))
L3²= 2 • 64 • 1,5
L3²= 3 • 64
L3=√3 • 64
L3= 8√3 cm
an= R • cos (180°/n)
a3= 8 • cos (180°/3)
a3= 8 • cos 60°
a3= 8 • 0,5
a3= 4 cm
Resposta: L= 8√3 cm e a= 4 cm
Questão 5)
I) Primeiramente, determinaremos o raio da circunferência.
A= πR²
25π= πR²
R²= 25π/π
R²= 25
R= √25
R= 5 cm
II) Agora, devemos determinar o ângulo central do polígono em questão, sabendo que o hexágono tem seis lados e o raio da sua circunferência inscrita mede 5 cm. Logo, teremos:
ac= 360°/ 6
ac= 360°/ 6
ac= 60°
Utilizando a fórmula geral do lado de um polígono regular inscrito e relembrando que R= 8 cm, teremos:
Ln²= 2R² • (1 - cos ac)
L6²= 2 • 5² • (1 - cos 60°)
L6²= 2 • 25 • (1 - 0,5)
L6²= 2 • 25 • 0,5
L6²= 25
L6=√25
L6= 5 cm
III) Sabendo a medida do lado do hexágono, basta multiplicá-la pelo número de lados do hexágono (n=6)
2p= 6 • L6
2p= 6 • 5
2p= 30 cm
Resposta: Item e.
Primeiramente, devemos determinar o ângulo central do polígono em questão, sabendo que o decágono tem dez lados. Logo:
ac= 360°/ 10
ac= 360°/ 10
ac= 36°
Utilizando a fórmula geral do lado de um polígono regular inscrito temos:
Ln²= 2R² • (1 - cos ac)
L10²= 2 • 6² • (1 - cos 36°)
L10²= 2 • 36 • (1 - 0,81)
L10²= 2 • 64 • 0,19
L10²= 13,68
L10=√13,68
L10= 3,7 cm
Questão 2)
I) Sabendo que o apótema deste hexágono mede 5√3 cm e que o hexágono regular apresenta 6 lados, devemos determinar a medida do raio de um polígono deste por meio da fórmula geral do apótema.
a6= R • cos (180°/n)
5√3= R • cos (180°/6)
5√3= R • cos (180°/6)
5√3= R • cos 30°
5√3= R√3
2
R√3= 5√3 • 2
R√3= 10√3
R= 10 cm
II) Utilizando a fórmula geral do lado de um polígono regular inscrito, teremos:
Ln²= 2R² • (1 - cos ac)
L6²= 2 • 10² • (1 - cos 60°)
L6²= 2 • 10² • (1 - 0,5)
L6²= 2 • 10² • 0,5
L6²= 10²
L6=√10²
L6= 10 cm
III) Agora que a medida do lado deste polígono é conhecida, teremos:
2p= 10 • 6
2p= 60 cm
Resposta: 2p= 60 cm
Questão 3)
I) Primeiramente, devemos determinar o ângulo central do polígono em questão, sabendo que o hexágono tem dez lados. Logo, teremos:
ac= 360°/ 6
ac= 360°/ 6
ac= 60°
Utilizando a fórmula geral do lado de um polígono regular inscrito e sabendo que o R= 12 cm, teremos:
Ln²= 2R² • (1 - cos ac)
L6²= 2 • 12² • (1 - cos 60°)
L6²= 2 • 144 • (1 - 0,5)
L6²= 2 • 144 • 0,5= 144
L6²= 144
L6=√144
L6= 12 cm
II) A apótema será dada por:
a6= R • cos (180°/n)
a6= 12 • cos (180°/6)
a6= 12 • cos 30°
a6= 12√3
2
a6=6√3 cm
Resposta: L= 12 cm e a= 6√3 cm
Questão 4)
Primeiramente, devemos determinar o ângulo central do polígono em questão, sabendo que o triângulo equilátero tem três lados e o raio da sua circunferência inscrita mede 8 cm. Logo, teremos:
ac= 360°/ 3
ac= 360°/ 3
ac= 120°
Utilizando a fórmula geral do lado de um polígono regular inscrito e relembrando que R= 8 cm, teremos:
Ln²= 2R^2 • (1 - cos ac)
L3²= 2 • 8^2 • (1 - cos 120°)
L3²= 2 • 64 • (1 - (-0,5))
L3²= 2 • 64 • 1,5
L3²= 3 • 64
L3=√3 • 64
L3= 8√3 cm
an= R • cos (180°/n)
a3= 8 • cos (180°/3)
a3= 8 • cos 60°
a3= 8 • 0,5
a3= 4 cm
Resposta: L= 8√3 cm e a= 4 cm
Questão 5)
I) Primeiramente, determinaremos o raio da circunferência.
A= πR²
25π= πR²
R²= 25π/π
R²= 25
R= √25
R= 5 cm
II) Agora, devemos determinar o ângulo central do polígono em questão, sabendo que o hexágono tem seis lados e o raio da sua circunferência inscrita mede 5 cm. Logo, teremos:
ac= 360°/ 6
ac= 360°/ 6
ac= 60°
Utilizando a fórmula geral do lado de um polígono regular inscrito e relembrando que R= 8 cm, teremos:
Ln²= 2R² • (1 - cos ac)
L6²= 2 • 5² • (1 - cos 60°)
L6²= 2 • 25 • (1 - 0,5)
L6²= 2 • 25 • 0,5
L6²= 25
L6=√25
L6= 5 cm
III) Sabendo a medida do lado do hexágono, basta multiplicá-la pelo número de lados do hexágono (n=6)
2p= 6 • L6
2p= 6 • 5
2p= 30 cm
Resposta: Item e.
Agradecimentos:
Agradeço a todos que prestigiaram o meu blog e espero que gostem das atuais e futuras postagens. Quem tiver dúvidas, pode comentá-las. Espero ter ajudado.
Referências:
1-https://mundoeducacao.bol.uol.com.br/matematica/apotema.htm
2-https://blogdoenem.com.br/calculo-do-lado-e-do-apotema-de-alguns-poligonos-regulares-matematica-enem/
3-https://www.infoescola.com/matematica/area-de-poligonos-regulares/
4-https://pt.wikipedia.org/wiki/Ap%C3%B3tema
5-https://alunosonline.uol.com.br/matematica/Area-poligono-regular.html
6-https://www.ime.unicamp.br/~chico/ma092/ma092_10_geo_pol_regulares.pdf
7-https://www.calcularporcentagem.net/como-calcular-area-do-poligono-regular/
8-https://www.stoodi.com.br/blog/2018/06/19/poligonos-regulares/
9-https://docplayer.com.br/27202577-3o-bimestre-geometria-autor-leonardo-werneck.html
10-https://www.youtube.com/watch?v=xQ5PJmnV580
11-http://matprofrenatas.blogspot.com/2012_03_11_archive.html
12-https://www.youtube.com/watch?v=N0pMTfKoF-o
13-https://pt.wikipedia.org/wiki/Pol%C3%ADgono_regular
14-https://www.oblogdomestre.com.br/2015/12/inscritoOucircunscrito.Matematica.html
15-https://www.stoodi.com.br/exercicios/ifrj/outros/questao/o-perimetro-de-um-hexagono-regular-inscrito-em-um-circulo-de/
16-http://nsaulasparticulares.com.br/wp-content/uploads/2014/07/Poligonos-regulares-inscritos-e-circunscritos.pdf
17-https://canal.cecierj.edu.br/052019/df45c26ca50e31a43758284df00d61b6.pdf
Referências:
1-https://mundoeducacao.bol.uol.com.br/matematica/apotema.htm2-https://blogdoenem.com.br/calculo-do-lado-e-do-apotema-de-alguns-poligonos-regulares-matematica-enem/
3-https://www.infoescola.com/matematica/area-de-poligonos-regulares/
4-https://pt.wikipedia.org/wiki/Ap%C3%B3tema
5-https://alunosonline.uol.com.br/matematica/Area-poligono-regular.html
6-https://www.ime.unicamp.br/~chico/ma092/ma092_10_geo_pol_regulares.pdf
7-https://www.calcularporcentagem.net/como-calcular-area-do-poligono-regular/
8-https://www.stoodi.com.br/blog/2018/06/19/poligonos-regulares/
9-https://docplayer.com.br/27202577-3o-bimestre-geometria-autor-leonardo-werneck.html
10-https://www.youtube.com/watch?v=xQ5PJmnV580
11-http://matprofrenatas.blogspot.com/2012_03_11_archive.html
12-https://www.youtube.com/watch?v=N0pMTfKoF-o
13-https://pt.wikipedia.org/wiki/Pol%C3%ADgono_regular
14-https://www.oblogdomestre.com.br/2015/12/inscritoOucircunscrito.Matematica.html
15-https://www.stoodi.com.br/exercicios/ifrj/outros/questao/o-perimetro-de-um-hexagono-regular-inscrito-em-um-circulo-de/
16-http://nsaulasparticulares.com.br/wp-content/uploads/2014/07/Poligonos-regulares-inscritos-e-circunscritos.pdf
17-https://canal.cecierj.edu.br/052019/df45c26ca50e31a43758284df00d61b6.pdf
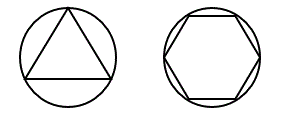

Nenhum comentário:
Postar um comentário