Área dos polígonos regulares

O que são polígonos regulares?

Polígonos são figuras geométricas formadas por linhas fechadas, que por sua vez são constituídas por segmentos de reta que não se cruzam e que estão em um mesmo plano. Eles podem ser classificados em polígonos regulares e irregulares. Esta classificação é dada em função do tamanho dos lados e de seus ângulos. Polígonos regulares possuem ângulos e lados congruentes, enquanto os polígonos irregulares apresenta estas medidas com valores distintos.Além disso, estas figuras podem ser convexas e não convexas. Se os ângulos que formam o polígono forem menores que 180°, o polígono será regular. Caso os ângulos sejam maiores que 180°, o polígono será não convexo. Tendo estes conhecimentos em vista, abordaremos o cálculo do lado e da apótema de um polígono regular

Fórmula geral da área de um polígono regular

Todo polígono regular pode ser inscrito em uma circunferência. Por sua vez, estas figuras podem ser decompostas, formando vários regiões triangulares. Dividindo o polígono em "n" triângulos idênticos, calculamos a área de cada um deles e multiplicamos pelo número de triângulos.
A área de cada triângulo é dada por:

At= L • h
2

Onde:
L=> Lado do polígono
h=> altura

*Obs: O número de lados do polígono é igual ao número de triângulos que o compõem.

Observando o hexágono inscrito abaixo, é possível perceber que a altura de cada triângulo corresponde ao apótema deste polígono. Logo a área de cada triângulo é:

At= L • a
2

A área do polígono será dada ao multiplicarmos a expressão acima pelo número de lados do polígono. Com isso, temos:

Ap= n • At

Ap= n • L • a
2

Sendo o perímetro do polígono P= n • L, teremos:

At= P • a
2

Se a medida do apótema não for dada, devemos encontrá-la.

Fonte:https://brasilescola.uol.com.br/matematica/poligonos-regulares-circunferencia.htm

Apótema

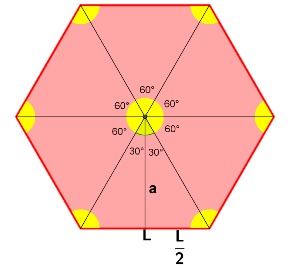
Para calcular a fórmula do apótema, consideremos um hexágono regular cujo lado mede 10 cm.

Fonte:https://www.infoescola.com/matematica/area-de-poligonos-regulares/

Primeiramente, devemos descobrir o ângulo de onde sai o apótema, ou seja, o ângulo central da figura. Para isso, basta dividir 360° pelos seis lados. Com isso, obteremos 60°.

ac=   360° = 360°
n 6

ac=60°

Por sua vez, o apótema sempre divide esse ângulo por outros dois de mesma medida. Neste caso, teremos 30°.
Feito isso, podemos aplicar um pouco de trigonometria para solucionar o problema.

tg 30°=  (L/2)
a

a • tg 30°=   L
2

2a • tg 30°= L

a= L
2 • tg 30°

Sendo L= 10 cm, teremos:

a= 10 = 3  •   10 = 30
2 • √3 2 • √3 2√3
3

a=   30    •   √3   =   30√3
2√3   √3 6

a=5√3 cm

Generalizando o caso para um polígono regular de lado L, apótema a. O ângulo do apótema, ou ângulo central, é dado por 360°/ n. Como devemos dividir este ângulo por dois para poder recorrer a trigonometria, teremos:

360°

a'= n = 360° • 1

2 n 2

a'= 180 °

Fonte:https://www.infoescola.com/matematica/area-de-poligonos-regulares/

tg (180°/n)= (L/2)

a • tg (180°/n)= L

a= L

2 • tg (180°/n)

Tendo em vista esta relação entre lado e apótema, podemos substituí-la na fórmula de área de modo a tornar fórmula mais simplificada. Com isso, teremos que a área de um polígono pode ser escrita como:

Ap= n •  L • a
2

Ap= n • L  • a
2
Ap=  n • L   •    L
2 2 • tg (180°/n)

Ap=   n • L²

4 • tg (180°/n)

Exemplo: Determine a medida da área de um hexágono regular cujo lado mede 10√3 m.

*Tendo em vista que o lado do hexágono foi dado e sabemos que o hexágono possui seis lados, basta substituir estes valores na fórmula simplificada da área de um polígono regular.
n=6 lados e L=200√3 m

Ap= n • L²

4 • tg (180°/n)

Ap= 6 • (10√3)²

4 • tg (180°/6)

Ap= 6 • 300

4 • tg 30°

Ap= 300 = 3 • 300 = 900

4 • √3 4 • √3 4√3

Ap= 225 = 225 • √3

√3 √3 √3

Ap= 225√3

Ap=75√3 m²

Agradecimentos:

Agradeço a todos que prestigiaram o meu blog e espero que gostem das atuais e futuras postagens. Quem tiver dúvidas, pode comentá-las. Espero ter ajudado.