Inequação do segundo grau

O que é? 

Ao estudarmos equações do segundo grau, sempre lidamos com igualdades, ou seja, determinamos    uma relação de igualdade entre a variável e as suas raízes. Enquanto as equações quadráticas representam igualdades, as inequações do segundo grau são desigualdades escritas pela lei matemática com forma ax² + bx + c,onde a, b e c pertencem ao conjunto dos números reais e a ≠ 0, acompanhada de um sinal de desigualdade.
As inequações do segundo grau podem ser escritas nas seguintes formas:

ax² + bx + c > 0
ax² + bx + c < 0
ax² + bx + c ≥ 0
ax² + bx + c ≤ 0

 Resolução:

Para resolver uma inequação do segundo grau, devemos aplicar a fórmula de Bhaskara para determinar suas raízes. Depois, devemos determinar a condições de existência da inequação em função do seu sinal de desigualdade e suas raízes. Veja alguns exemplos:

                                 
Exemplo 1: x² + x - 2 > 0
I) Primeiramente, resolveremos a inequação pela fórmula de Bháskara:
∆= b² - 4ac
∆= (1)² - 4 • 1 • (-2)
∆= 1 + 8                                                                                
∆= 9

x=  -1 ± √9 
       2 • 1

x= -1 ± 3  
        2
x'=  -1 + 3 
          2

x'= 1

x"= -1- 3 
         2
x"= -2

II) O estudo do sinal desta inequação é dada pelo seguinte gráfico:                            

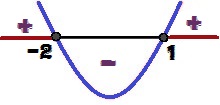
          Estudo do sinal de x² + x - 2 > 0 

Fonte:https://alunosonline.uol.com.br/matematica/inequacao-2-grau.html

*Logo, concluímos que os valores de x para os quais a inequação vai ser maior que zero são os números reais tais que x > 1  ou x < -2. O conjunto solução da inequação será:

     

Resposta: {x ∈ IR| x > 1 ou x < -2}

Exemplo 2: -2x² - x + 1 ≤ 0
I) Primeiramente, resolveremos a inequação pela fórmula de Bháskara:
∆= b² - 4ac
∆= (-1)² - 4 • (-2) • (1)
∆= 1 + 8 
∆= 9 

x=   1 ± √9   
         2 •(-2)

x=  1 ± 3 
        (-4)

x'=  1 + 3  = (4)  = -1
        (-4)      (-4)                                                  
           

x"=  1 - 3  =  (-2)  = (1/2)
         (-4)       (-4)


II) O estudo do sinal desta inequação é dada pelo seguinte gráfico:  

                                                  Estudo do sinal de -2x² - x + 1 ≤ 0      

Fonte:https://brasilescola.uol.com.br/matematica/inequacao-segundo-grau.htm
                                   
*Como a inequação quer valores maiores ou iguais a 0, escrevemos que o conjunto solução da inequação será:

S= {x ∈ IR| x ≤ -1 ou x ≥ -1/2 }

Resposta:{x ∈ IR| x ≤ -1 ou x ≥ -1/2}

Exercícios:                                                  

Questão 1)(UDESC  2008) - O conjunto solução da inequação x² - 2x - 3 ≥ 0 é:                        
a){x ∈ IR| -1 < x <  3}                                   
b) {x ∈ IR| -1 < x ≤ 3}         
c) {x ∈ IR| x < -1  ou  x > 3}       
d) {x ∈ IR| x ≤ -1  ou  x > 3}                        
e) {x ∈ IR| -1 ≤ x ≤ 3}
              
Questão 2) O conjunto solução da inequação (x - 2)² > 2x - 1, considerando como conjunto universo o conjunto dos reais, está definido por:
a) 1 < x < 5
b) 3 < x < 5
c) 2 < x < 4
d) 1 < x < 4                                                      
e) 2 < x < 5    

Questão 3)(PUC-RIO 2009) Quantas soluções inteiras a inequação 
x²+ x - 20 ≤ 0 admite?
a) 2
b) 3
c) 7
d) 10
e) 13

Questão 4) Resolva a seguinte inequação:     x² + x - 6     ≥  0                                          
                                                                       2x² + 3x - 2
                                                             
                       
Questão 5)  Resolva a seguinte inequação 
(x² - 3x + 10) •  (-x² + 7x - 6) < 0

Resoluções:        

Questão 1)
I) Primeiramente, resolveremos a inequação pela fórmula de Bháskara:

x² -2x -3 ≥ 0

∆= b² - 4ac
∆= (-2)² - 4 • (1) • (-3)
∆= 4 + 12
∆= 16

x=   2 ± √16  
         2 •(1)

x=  2 ± 4 
         2

x'=  2 + 4  =  6  = 3
          2         2

x"= 2 - 4  =  (-2)  = -1
         2            2    

II)  O estudo do sinal da inequação desta questão é dado pelo seguinte gráfico:                                 

                                         Estudo do sinal de x^2 - 2x - 3 ≥ 0                                        

*Com isso, concluímos que os valores de x para os quais a inequação vai ser maior ou igual a 0 são os números reais tais que  -1 ≤ x ≤ 3. O conjunto solução da inequação será:                                   

S= {x ∈ IR| -1 ≤ x ≤ 3}                                                                                

Resposta: Item e.

Questão 2)           
I) Desenvolvendo o quadrado da diferença no primeiro lado da desigualdade, teremos:
(x - 2)² > 2x - 1                 
x² - 4x + 4 > 2x -  1
x² - 4x - 2x + 4 + 1 > 0
x² - 6x + 5 > 0

II) Resolvendo a inequação pela fórmula de Bháskara:
∆= b² - 4ac
∆= (-6)² - 4 • 1 • 5
∆= 36 - 20
∆= 16                             

x=  6 ± √16  
        2 • 1

x= 6 ± 4 
        2

x'= 6 + 4  =  10  = 5
         2          2

x"= 6 - 4  =   2  = 1
          2         2


II) O estudo do sinal da inequação é dado pelo seguinte gráfico:

                                                   Estudo do sinal de (x - 2)^2 > 2x - 1


 
*Com isso, concluímos que os valores de x para os quais a inequação vai ser menor que zero são os números reais tais que 1 < x < 5. O conjunto solução da inequação será:

S={x ∈ IR| 1 < x < 5 }         

Resposta: Item a

Questão 3)                    

I) Primeiramente, resolveremos a inequação pela fórmula de Bháskara:

x² + x - 20 ≤0

∆= b^ 2 - 4ac
∆= (1)^ 2 - 4 • (1) • (-20)
∆= 1 + 80
∆= 81

x=  -1 ± √81  
         2 •(1)

x=  -1 ± 9 
          2

x'= -1 + 9  = 8  = 4
          2         2

x"= -1 - 9  =  (-10)  = -5
          2             2 

II) O estudo do sinal da desigualdade é dado pelo seguinte gráfico:

                                                 Estudo do sinal  de x^2 + x - 20 ≤ 0


 
*A partir deste gráfico, concluímos que os valores de x para os quais a inequação vai ser menor ou igual zero são os números reais tais que  -5 ≤ x ≤ 4. O conjunto solução da inequação será:

S={x ∈ IR|-5 ≤ x ≤ 4 }

III) Como queremos os inteiros para os quais x^2 + x - 20 ≤ 0, temos que saber os inteiros entre -5 e 4.  São eles: -5, -4,  -3, -2, -1, 0, 1,  2, 3, 4. Com isso, sabemos agora que existem 10 soluções inteiras para a inequação.

Resposta: Item d.

Questão 4)

I) Por se tratar de uma inequação quociente, devemos resolver separadamente as duas equações. Façamos y1= x² + x - 6  e  y2= 2x² + 3x - 2. Feito isso, resolveremos y1 pela fórmula de Bháskara.

∆= b² - 4ac
∆= (1)^ 2 - 4 • (1) • (-6)
∆= 1 + 24
∆= 25

x=   -1 ± √25  
         2 •(1)

x=   -1 ± 5
           2

x'= -1 + 5  = 4  = 2
         2          2

x"=  -1 - 5  =  (-6)  = -3
           2            2
                        

II) O estudo do sinal de y1 é dado pelo seguinte gráfico:

                              

III)Resolveremos y2  pela fórmula de Bháskara:
∆= b² - 4ac
∆= (3)² - 4 • (2) • (-2)
∆= 9 + 16
∆= 25

x=  -3 ± √25  
         2 •(2)

x=  -1 ± 5 
          4

x'= -3 + 5  = 2  =  1 
          4         4      2

x"= -3 - 5  =  (-8)  = -2
          4            4 

IV) O estudo do sinal de y2 é dado pelo seguinte gráfico:

V) Por fim, realizaremos o estudo do sinal do quociente:

*Como a inequação quer valores maiores ou iguais a 0, escrevemos que o conjunto solução da inequação será:

S={x ∈ IR|x ≤ -3 ou -2 < x  < 1/2  ou  x ≥ 2}

Questão 5)

I) Por se tratar de uma inequação produto, devemos resolver separadamente as duas equações. Façamos y1= x² - 3x - 10  e  y2= -x² + 7x - 6. Feito isso, resolveremos y1 pela fórmula de Bháskara.

∆= b² - 4ac
∆= (-3)² - 4 • (1) • (-10)
∆= 9 + 40
∆= 49

x=   3 ± √49  
         2 •(1)

x=   3 ± 7
          2

x'= 3 + 7  = 10  = 5
         2          2

x"=  3 - 7  =  (-4)  = -2
          2            2                                                                                                                                                                                                                                                                                                            

II) O estudo do sinal de y1 é dado pelo seguinte gráfico:

 III)Resolveremos y2 pela fórmula de Bháskara:
∆= b² - 4ac
∆= (7)^ 2 - 4 • (-1) • (-6)
∆= 49 - 24
∆= 25

x=  -7 ± √25  
         2 •(-1)

x=  -7 ± 5 
         (-2)

x'= -7 + 5  =  (-2)  = 1
        (-2)        (-2)

x"= -7 - 5  =  (-12)  = 6
         (-2)        (-2)                                                 

IV) O estudo de y2 é dado pelo seguinte gráfico:

VI) Por fim, realizaremos o estudo do sinal do produto para encontrarmos:

*Como a inequação quer valores menores que zero, escrevemos que o conjunto solução da inequação será: 
S={x ∈ IR|x < -2 ou 1 < x  < 5  ou  x > 6}   

Agradecimentos:

Agradeço a todos que prestigiaram o meu blog e espero que gostem das atuais e futuras postagens. Quem tiver dúvidas, pode comentá-las. Espero ter ajudado.                                

                                                                           
                                                                                                                                  

Referências:

1-https://socratic.org/questions/how-do-i-convert-the-equation-f-x-x-2-4x-3-to-vertex-form 
2-https://alunosonline.uol.com.br/matematica/inequacao-2-grau.html 
3-https://www.infoescola.com/matematica/inequacao-do-segundo-grau/ 
4-https://brasilescola.uol.com.br/matematica/inequacao-segundo-grau.htm
5-https://mundoeducacao.bol.uol.com.br/matematica/condicoes-uma-inequacao-2-grau.htm
6-https://educacao.uol.com.br/disciplinas/matematica/inequacoes-do-segundo-grau-exemplos-de-resolucao.htm
7-https://exercicios.brasilescola.uol.com.br/exercicios-matematica/exercicios-sobre-inequacao-2-o-grau.htm 
8-http://www.matematicadidatica.com.br/FuncaoQuadraticaVariacaoSinal.aspx
9-https://www.infoescola.com/matematica/inequacao-do-segundo-grau/exercicios/
10-https://sabermatematica.com.br/exercicios-resolvidos-inequacao-do-segundo-grau.html