Função do segundo grau

O que é uma função do segundo grau?

É toda função f: R --> R escrita na forma f(x)= ax² + bx + c com a≠0; Sendo que os coeficientes a, b, c são números reais. Quando uma função quadrática é escrita em um gráfico, ela é representada por uma parábola. Os coeficientes destas funções são importantes para a interpretação delas, visto que eles fornecem diversas informações sobre os seus gráficos.

Exemplos:

1) f(x) = x² + 5x + 6, onde a=1; b=5; c= 6

2) f(x)= -x² - 6 onde a= -1; b= 0; c= -6

3) f(x)= -x² + 8x onde a= -1; b= 8; c=0

Gráfico da função do segundo grau:

Como explicado anteriormente, o gráfico descrito pela função quadrática no plano cartesiano é uma parábola e os coeficientes destas funções fornecem informações importantes para seu estudo e compreensão.

As mais importantes informações são:

Concavidade da parábola:

O coeficiente a determina a característica mais importante da parábola: a sua concavidade. Ela é determinada quando:

Resultado de imagem para função do segundo grau

Fonte:https://brasilescola.uol.com.br/matematica/grafico-funcao.htm

a> 0 - concavidade da parábola voltada para cima

a<0 - concavidade da parábola voltada para baixo

Zeros:

Os valores de x nos quais a função quadrática se anula, ou seja, para os quais f(x)= 0 são conhecidos como zeros da função quadrática e indicam os pontos onde a parábola interceptará o eixo x (eixo das abscissas). Isso é válido somente quando as raízes forem números reais, pois caso não sejam, o gráfico não interceptará o eixo x.
Os zeros são as raízes de uma equação do segundo grau, ou seja, determinar estes números equivale a resolver uma equação do segundo grau ax² + bx + c= 0.

Estas equações podem ser resolvidas por diversos métodos, sendo que o mais conhecido é a fórmula de Bhaskara, que é dada por:

x= -b ± √∆
2a

Sendo ∆= b² - 4ac, podemos ter as seguintes situações:

∆ > 0 - A parábola intercepta o eixo x em dois pontos distintos
∆ = 0 - A parábola é tangente ao eixo x
∆ < 0 - A parábola não intercepta o eixo x

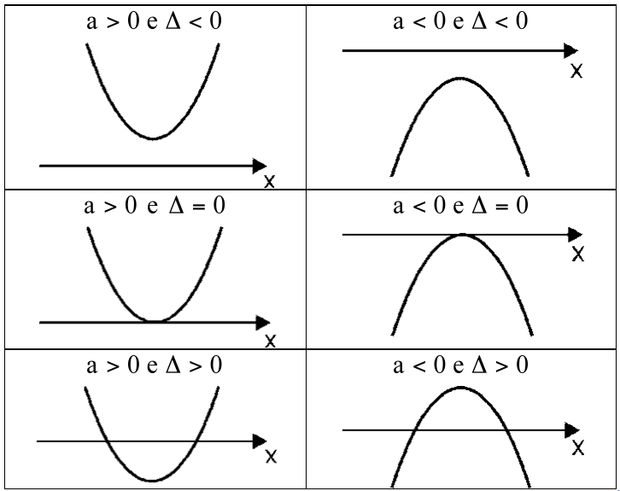
Fonte:http://educacao.globo.com/matematica/assunto/funcoes/funcao-de-2-grau.html

Intersecção da parábola com o eixo y (eixo das ordenadas):

Quando x= 0, a parábola interceptará o eixo das ordenadas porque y= a • 0^2 + b • 0 + c= c. Por conta disso, a parábola interceptará o eixo das ordenas no ponto (0, c).

Vértice da parábola:

O vértice da parábola representa o ponto mínimo ou máximo da função quadrática. Ele será determinado pelo par ordenado (xv, yv).

Para determinar xv, basta considerar que o ponto de simetria passa pelo vértice e é equidistante às raízes, temos xv.

Então, xv será:

xv = x' + x''

   2
O ponto xv também pode ser calculado como:

xv = - b
2a

O ponto yv é dado por:

yv= - b² - 4ac = - ∆
    4a 4a

Fonte: https://alunosonline.uol.com.br/matematica/grafico-da-funcao-do-2-grau.html

Dominando o conhecimento - Exercícios:

Questão 1) Encontre o valor de f(x)= x² + 3x - 10 para que f(x)=0,

Questão 2) Determine os pontos de intersecção da parábola da função f(x)= 2x² - 3x + 1 com o eixo das abscissas.

Questão 3) O gráfico da função quadrática definida por
y= x² - mx + (m-1), em que m ∈ R, tem um único ponto em comum com o eixo eixo das abscissas. Determine y associado ao valor de x=2.

Questão 4) Calcule o valor de k de modo que a função f(x)= 4x² - 4x - k não tenha raízes, isto é, o gráfico não tem pontos em comum com o eixo x.

Questão 5) (UfSCar - SP) Uma bola ao ser chutada num tiro de meta por um goleiro, numa partida de futebol, teve sua trajetória descrita pela equação h(t)=-2t²+ 8t (com t igual ou maior que zero), onde t é o tempo medido em segundos e h(t) é a altura em metros da bola no instante t. Determine após o chute.
a) O instante em que a bola retornará ao solo
b) A altura máxima atingida pela bola

Questão 6) Sabe-se que o custo de C (em reais) para produzir x unidades de certo produto é dado pela expressão C= x² - 80 x + 3000. Calcule a quantidade de unidades produzidas para que o custo seja mínimo e o valor desse custo seja mínimo.

Resoluções:

Questão 1)
I) Para que f(x)=0, obteremos a seguinte equação:

f(x)=0

x² + 3x - 10= 0

Coeficientes da equação
a=1
b=3
c= -10

II) Analisando a função e visto que ela deve ser igual a zero, podemos obter os zeros da função através da fórmula de Bhaskara

∆=b² - 4ac
∆= (3)² - 4 • 1• (-10)
∆=9 + 40
∆=13

x= -b ± √∆

2a

x=-(3)± √49
2 • 1

x= -3 ± 7
2

x'=-3 + 7
2
x'= 4
2

x'=2

x''= -3 - 7
2

x''= - 10
2

x''= -5

Resposta: Os dois valores para os quais f(x)=0 são x'=3 e x''= -5.

Questão 2)
I) Como os pontos que interceptam o eixo das abscissas correspondem aos valores para os quais f(x)=0, temos a segui

f(x)=0

2x² - 3x + 1= 0

Coeficientes da equação
a=2
b= -3
c= 1

II) Analisando a função e visto que ela deve ser igual a zero, podemos obter os zeros da função através da fórmula de Bhaskara

∆=b² - 4ac
∆= (-3)² - 4 • 2• (1)
∆=9 - 8
∆=1

x= -b ± √∆

2a

x=-(-3)± √1
2 • 2

x= 3 ± 1
4

x'= 3 + 1
4
x'= 4
4

x'=1

x''= 3 - 1
4

x''= 2
4

x''= 1/2

Resposta: Os dois pontos nos quais a parábola interceptam o eixo das abscissas são x'=1 e x''=1/2.

Questão 3)
I) Quando a parábola possui um ponto em comum com o eixo x, significa que a função possui apenas uma raiz e que ∆= 0. Considerando a função da questão e seus coeficientes, temos que:

∆=b² - 4ac
(-m)² - 4 • 1 • (m+1)=0
m^2 - 4m - 4= 0

II) Aplicando a fórmula de Bhaskara, temos os seguintes valores para m

m= -b ± √∆

2a

m=-(-4)± √0
2 • 1

m= 4 ± 0
2

m= 4
2

m=2

III) Substituindo m=2, obtemos a lei desta função:

y= x² - mx + (m-1)
y= x² - 2x + (2-1)
y= x² - 2x + 1
IV) Como a questão exige o valor de y quando x=2, a resposta será:
x=2
y=x² - 2x + 1
y=2² - 2 • 2 + 1
y= 4 - 4 + 1
y=1

Resposta: A função possui a lei de formação y= x² - 2x + 1 e quando temos x=2, y será igual a 1.

Questão 4)
I) Quando a parábola possui não intercepta o eixo x, significa que ela não possui raízes reais e que
∆ < 0. Considerando a função da questão e seus coeficientes, temos que:

∆=b² - 4ac
(4)² - 4 • 4 •( -k )< 0
16 + 16k < 0
16k < -16
k < -16
16
k < -1

Resposta: O valor de k para que a função não possua raízes deve ser menor que -1.

5 (item a)
I)Houve dois momentos em que a bola tocou o chão, o primeiro foi antes dela ser chutada e o segundo foi quando ela terminou sua trajetória.

h(t)= - 2t² + 8t
0= -2t² + 8t
2t² - 8t=0
2t(t -4)=0
t'=0
t''-4=0
t''= 0 + 4
t''= 4 s

Resposta: A bola retornará ao solo após 4 segundos do seu lançamento

Questão 5(item b)
I) A altura máxima atingida pela bola é dada pelo vértice da parábola. As coordenadas do vértices podem ser encontradas através das seguintes expressões:

xv= - b
2a

yv= - b² -4ac = - ∆
4a 4a

II) Neste caso, é necessário encontrar yv, visto que ele determina a altura máxima atingida pela bola.

yv= - b² - 4ac = -  ∆
4a 4a

yv= - (8)² - 4 • (-2) • 0
4 • (-2)

yv= - 64
- 8

yv= 8 metros

Resposta: A altura máxima atingida pela bola foi igual a 8 metros.

Questão 6)
I) O número de peças para que o custo seja mínimo será dado ao determinarmos o valor de xv na função. Sabendo que C= x² - 80 x + 3000, o valor de xv será:

xv= - b
         2a
xv = - (-80)
           2 • 1

xv= 80
   2

xv= 40

II) Tendo em vista que o número de peças para o custo mínimo é conhecido, o valor desse custo será dado ao substituirmos xv na função. Logo, o custo mínimo de produção será:
C= x² - 80 x + 3000
C= 40² - 80 • 40 + 3000
C=1600 - 3200 + 3000
C= 1600 - 200
C= 1400

Resposta: Para obter um custo mínimo de R$ 1400,00 a empresa deverá produzir exatamente 40 peças.


Fonte: http://www.sustente.org.br/attachments/article/31/Y-PROVAProfessorIIMatematica.pdf

Agradecimentos:

Agradeço a todos que prestigiaram meu blog e espero que gostem das atuais e futuras postagens do blog. Quem tiver dúvidas, pode comentá-las. Espero ter ajudado.