Fórmula de Herão

Introdução:

Heron de Alexandria foi um matemático e engenheiro responsável por elaborar uma fórmula que determina a área de um triângulo em função dos seus três lados. Esta fórmula é conhecida como fórmula de Heron e ela é muito útil nos casos em que não temos a altura de um triângulo, mas somente as medidas dos seus lados.

A expressão da fórmula de Heron é escrita como:

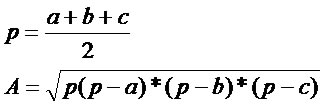
Sendo a, b, c são os lados deste triângulo e p é o seu semiperímetro.

Exemplo 1: Determine a área do triângulo abaixo.

Fonte:https://casadamatematica.com.br/entendendo-teorema-de-herao/

* Visto que as medidas dos lados do triângulo acima são conhecidas, devemos utilizar a fórmula de Heron para determinar a sua área

p=  a + b + c  

            2

p=  3 + 4 + 5 =  12  

            2             2

p= 6 cm

A= √p • (p - a) • (p - b) • (p - c)
A= √6 • (6 - 4) • (6 - 5) • (6 - 3)
A= √6 • 2 • 1 • 3=√6 • 6
A= √36
A= 6 cm²

Resposta: A área deste triângulo é igual a 6 cm^2.

Exemplo 2: Utilizando a Fórmula de Heron, calcule a área da região com as medidas: 26 cm, 26 cm e 20 cm

* Como a região mencionada forma um triângulo cujos lados são conhecidos, a sua área pode ser facilmente calculada pela fórmula de Heron

p=  a + b + c  

            2

p=  26 + 26 + 20 =  72  

              2                 2

p= 36 cm

A= √p • (p - a) • (p - b) • (p - c)

A= √36 • (36 - 26) • (36 - 26) • (36 - 20)
A= √36 • (36 - 26) • (36 - 26) • (36 - 20)=  √36 • 10 • 10 • 16
A= √57600
A= 240 cm²

Resposta: A área desta região é igual a 240 cm².

Exemplo 3: Calcule a área da região triangular com as medidas: 6 cm, 8 cm e 10 cm.

* Como a região mencionada forma um triângulo cujos lados são conhecidos, a sua área pode ser facilmente calculada pela fórmula de Heron

p=  a + b + c  

            2

p=  6 + 8 + 10   =  24  = 12 cm

             2                2

A= √p • (p - a) • (p - b) • (p - c)
A= √12 • (12 - 6) • (12 - 8) • (12 - 10)
A= √12 • 6 • 4 • 2
A= √576
A= 24 cm^2

Resposta: A área desta região triangular é igual a 24 cm².

Agradecimentos:

Agradeço a todos que prestigiaram o meu blog e espero que gostem das atuais e futuras postagens. Quem tiver dúvidas, pode comentá-las. Espero ter ajudado.

Referências:

1-https://mundoeducacao.bol.uol.com.br/matematica/formula-heron.htm

2-https://alunosonline.uol.com.br/matematica/formula-de-heron.html

3-https://www.resumoescolar.com.br/matematica/formula-de-heron/

4-https://ensinodematemtica.blogspot.com/2010/01/formula-de-heron-21012010.html

5-https://casadamatematica.com.br/entendendo-teorema-de-herao/

6-http://clubes.obmep.org.br/blog/b_heron-de-alexandria/