Desafios de matemática 7.0

Questão 1 - IME 2008) Um quadrado ABCD o segmento AB', com comprimento igual ao lado do quadrado, descreve um arco de círculo, conforme indicado na figura. Determine o ângulo BÂB' correspondente à posição em que a razão entre o comprimento do segmento B'C e o lado do quadrado vale √(3 -  √6).

                                                         

                       

  Fonte:https://www.tutorbrasil.com.br/forum/viewtopic.php?t=21431

Questão 2 -Ufrn 2000) Um observador, situado no ponto P de um prédio, vê três pontos, Q, R e S, numa mesma vertical, em um prédio vizinho, conforme esquematizado na figura abaixo. P e Q estão num mesmo plano horizontal, R está 6 metros acima de Q, e S está 24 metros acima de Q. Verifica-se que o ângulo RPQ do triângulo QPR é igual ao ângulo  do triângulo RPS. O valor, em metros, que mais se aproxima da distância entre P e Q é: 

a) 8,5 

b) 8,8 

c) 9,4 

d) 10,2

                         

Fonte da imagem: https://www.professor.bio.br/matematica/provas_vestibular.asp?origem=Ufrn&curpage=8

Questão 3- Mackenzie) No triângulo ABC temos AB = AC e sen x = 3/4. Então cos y é igual a: (imagem abaixo) 

a) 9/16 

b) 3/4 

c) 7/9 

d) 1/8 

e) 3/16

                                                                                     

Fonte:http://professor.bio.br/matematica/comentarios.asp?q=6350&t=Trigonometria

Questão 4-ITA 1973) Um navio, navegando em linha reta, passa sucessivamente pelos pontos A, B e c. Quando o navio está em A, o comandante observa um farol em L, e calcula o ângulo 

LÂC= 30º. Após navegar 4 milhas até B, verifica o angulo LBC = 75º. Quantas milhas separam o farol do ponto B?

a) 4

b) 2√2

c) 8/3

d)(√2)/2

e) Nenhuma das anteriores

Resoluções:

Questão 1 - IME 2008)

I) Pelo enunciado, obtemos a seguinte relação entre o segmento B'C e o lado do quadrado (L):

B'C/L= √(3 -  √6)

B'C=  √(3 -  √6) • L

II) Da reconstrução da figura, temos o ângulo B'ÂB= α, AC=L√2 por ser diagonal do quadrado ABCD e, pelo mesmo motivo, BÂC= 45°e  B'ÂC= 45° - α.

Aplicando a Lei dos Cossenos

B'C²= AB'² + AC² - 2 • AB' • AC • cos (45° - α)

[√(3 - √6) • L]²= L² + (L√2)² - 2 • L • L√2 • cos (45° - α)

(3 - √6) • L²= L² + 2L² - (2√2)L² • cos (45° - α)

(3 - √6) • L²= L² [3 - (2√2) • cos (45° - α)]

Dividindo tudo por L²:

3 - √6= 3 - (2√2) • cos (45° - α)

-√6= - (2√2) • cos (45° - α) 

√6= (2√2) • cos (45° - α) 

cos (45° - α)= (√6)/(2√2)= (√3)/2

cos (45° - α)= (√3)/2 =>  45°- α= ± 30°

 45°- α= ± 30° => α=15° ou α= 75°

Resposta:  α=15° ou α= 75°

Questão 2)

I) Denotando o lado QP como x e utilizando α= β juntamente com trigonometria, teremos:

tg (α)= RQ/QP= 6/x= y

tg (α + β)= SQ/QP= 24/x= 4 • (6/x)= 4y

tg (2α)= 24/x= 4y

II) Usando a relação do arco duplo da tangente

tg (2α)= 2tg (α)/(1 - tg² α)

tg (2α)= 2y/ (1 - y²)

4y= 2y/(1- y²)

[4y(1- y²)]/2y= 1

2(1- y²)=1

2 - 2 y²= 1 => y= 1/(√2)

Substituindo y= 6/x

6/x=1/(√2) => x=6√2 = 8,46 m (utilizando √2=1,41)

x~8,5 metros

Resposta: Item a

Questão 3- Mackenzie)

I) Sabendo que o triângulo ABC é isósceles e utilizando a soma dos ângulos internos de um triângulo, encontramos:

2x + y= 180 => y= 180 - 2x

cos y=cos (180 - 2x)= - cos (2x)

cos y= - cos (2x)= sen² x - cos² x (eq.i) 

II) Somando a relação relação fundamental da trigonometria com a equação i, encontramos:

*sen² x + cos² x= 1 (relação fundamental da trigonometria)

1 + cos y= sen² x + cos² x + sen² x - cos² x

1 + cos y= 2 • sen² x

cos y= 2 • sen² x - 1= 2 • (3/4)² - 1

cos y= 2 • (9/16) - 1= (18/16) - 1

cos y=(18-16)/16= 2/16

cos y= 2/16= 1/8

Resposta: cos y= 1/8. Item d.

Questão 4)

Dado: AB= 4 milhas (só para relembrar)

I) A situação descrita é representada pela seguinte imagem:

Fonte:https://pir2.forumeiros.com/t19471-questao-de-geometria

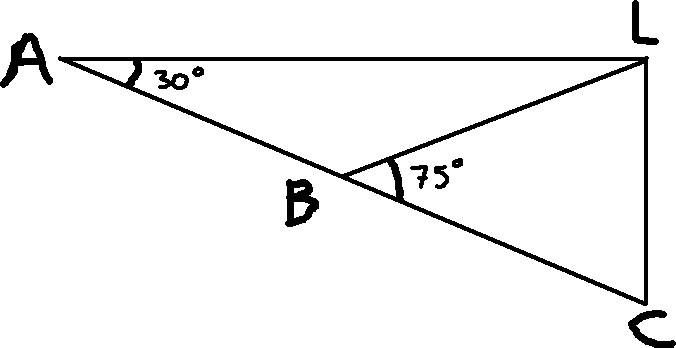
II) A partir do teorema do ângulo externo, encontramos o seguinte valor para o ângulo ALB:

LÂB + ALB= ABL

30° + ALB= 75° => ALB= 45°

III) A partir da lei dos senos:

AB/sen 45°= LB/ sen 30°

4/sen 45°= LB/ sen 30° 

Lembrando que sen 45°= (√2)/2 e sen 30°= 1/2

8/√2= 2LB => LB= 4/√2

-Racionalizando:

LB= (4√2)/2

LB= 2√2 milhas  => item b

Resposta: Item b

Agradecimentos:

Agradecimentos:

Agradeço a todos que prestigiaram o meu blog e espero que gostem das atuais e futuras postagens. Quem tiver dúvidas, pode comentá-las. Espero ter ajudado, principalmente em meio a esta situação da pandemia.

 

Relação fundamental da trigonometria

Introdução:

Uma importante relação da trigonometria é a relação fundamental, visto que outras podem ser demonstradas a partir dela e ela vale para quaisquer ângulos. Nesta postagem, será feita a demonstração desta importante relação.

Demonstração:

Seja ABC um triângulo retângulo, vale a seguinte relação entre suas medidas:

a²= b² + c² (Teorema de Pitágoras)

Fonte:https://pt.wikipedia.org/wiki/Ficheiro:Tri%C3%A2ngulo_Ret%C3%A2ngulo.jpg

Dividindo ambos os membros por a², teremos:

a²/a²=  (b² + c²)/ a²

1=  b²/a² + c²/a²

-A partir das relações trigonométricas do triângulo retângulo, temos que:

sen α= c/a

cos α= b/a

-Logo,

1=  b²/a² + c²/a² => 1= sen² α + cos² α  

* sen² α + cos² α= 1 (relação fundamental da trigonometria)  

Exemplo 1: Sendo sen θ= 0,6, com 0 ≤ x ≤ π/2 rad, calcule cos θ.

-A partir da relação fundamental, teremos:

sen² θ + cos² θ= 1

0,6² + cos² θ= 1

cos² θ= 1 - 0,36= 0,64

cos θ= √(0,64)

cos θ= 0,8

Resposta: cos θ= 0,8

Agradecimentos:

Agradeço a todos que prestigiaram o meu blog e espero que gostem das atuais e futuras postagens. Quem tiver dúvidas, pode comentá-las. Espero ter ajudado, principalmente em meio a este período de pandemia.

Arco duplo- demonstração

Introdução:

As relações de arco duplo são relações utilizadas nos cálculos das relações de seno, cosseno e tangente do dobro de um determinado ângulo conhecido. Elas podem ser demonstradas de diversas formas. Nesta postagem, será apresentada uma destas demonstrações.

Demonstração:

A partir dos triângulos ABC e ADC, que se encontram na imagem logo abaixo, obtém-se as seguintes relações

I) Do triângulo ABC, temos: tg θ= t/1= t

II) A partir do teorema do ângulo externo, encontramos que:

ângulo ADC= θ + θ =2θ

III) A partir do teorema de Pitágoras, teremos:

a²= (1 - a)² + t²

a²= 1- 2a + a² + t²

a² - a²= 1- 2a + t²  

0= t² - 2a + 1 

2a= t² + 1 => a= (t² + 1)/2

IV) Aplicando trigonometria no triângulo ADC, encontramos:

-Arco duplo do seno

sen 2θ= t/a= t/[(t² + 1)/2]

sen 2θ= 2t/(t² + 1)

Sendo t= tg θ, teremos:

sen 2θ= 2 tg θ/( tg² θ + 1)

-Sendo tg θ= sen θ/cos θ, t= tg θ e tg² θ + 1= sec² θ= (1/ cos² θ), teremos:

sen 2θ= [2(sen θ/cos θ)]/[(1/ cos² θ)]

sen 2θ= 2(sen θ/cos θ) • cos² θ

sen 2θ= 2 • sen θ • cos θ

- Arco duplo do cosseno

cos 2θ= (1-a)/a= [1- (t² + 1)/2]/[(t² + 1)/2]

cos 2θ= (2 - t² - 1)/ (t² + 1)

cos 2θ= (1 - t²)/ (t² + 1)

-Sendo tg θ= sen θ/cos θ, t= tg θ e tg² θ + 1= sec² θ= (1/ cos² θ), teremos:

cos 2θ= (1 - tg² θ)/ (tg² θ + 1)

cos 2θ= (1 - (sen θ/cos θ)²)/ (tg² θ + 1)

cos 2θ= ((cos² θ - sen² θ)/cos² θ)/(1/ cos² θ)

cos 2θ= ((cos² θ - sen² θ)/cos² θ) • cos² θ

cos 2θ= (cos² θ - sen² θ)

A partir do teorema fundamental da trigonometria, sen² θ + cos² θ  =1, temos que:

cos² θ  =1 - sen² θ

Substituindo na fórmula do arco duplo, temos

cos 2θ= (1 - 2sen² θ)

De forma análoga, encontramos:

sen² θ  =1 - cos² θ

Substituindo na fórmula do arco duplo, temos:

cos 2θ= (2cos² θ - 1)

Com isso, encontraram-se três fórmulas para o cosseno do arco duplo.

Tangente do arco duplo

 tg 2θ= t/(1- a)

Sendo a= (t² + 1)/2, teremos

 tg 2θ= t/(1- [(t² + 1)/2])

 tg 2θ= t/((2 - t² - 1)/2)

 tg 2θ= 2t/(1 - t²)

Substituindo t= tg θ, teremos:

 tg 2θ= 2tg θ/(1 - tg² θ)

Agradecimentos:

Agradeço a todos que prestigiaram o meu blog e espero que gostem das atuais e futuras postagens. Quem tiver dúvidas, pode comentá-las. Espero ter ajudado, principalmente em meio a esta situação da pandemia.