Desafios de Matemática 6.0

Desafio 1- (EFOMM 2011) Um hexágono regular regular de lado igual a 8 cm está inscrito na base de um cone de revolução de volume igual a 128π cm³. A razão entre a área total do cone e a área total de um cilindro, com o mesmo volume e a mesma base do cone é de:
a) 0,3
b) 0,6
c) 0,9
d) 0,27
e) 0,36

Desafio 2- (IME 2002) Um cone e um cilindro circulares retos têm uma base comum e o vértice do cone se encontra no centro da outra base do cilindro. 
Determine o ângulo formado pelo eixo do cone e sua geratriz, sabendo-se que a razão entre a área total do cilindro e a área total do cone é 7/4.

Desafio 3- (EFOMM 2011) Seja um contêiner, no formato de um paralelepípedo retângulo de dimensões a, b e c, a maior distância entre dois vértices do paralelepípedo é igual a 6√5 m. É correto afirmar que metade de sua área total é, em m², vale (a + b + c= 22 m):
a) 120
b) 148
c) 152
d) 188
e) 204

Resolução:

Desafio 1) (EFOMM 2011) 

I) Se um hexágono regular de 8 cm de lado está inscrito na base de um cone de revolução, significa que o raio da sua base mede 8 cm. Isso ocorre porque o lado de um hexágono regular inscrito em uma circunferência é igual ao raio da circunferência. 
Com isso, teremos:

R= L6
R= 8 cm

II) Sabendo o raio da base deste cone e o seu volume, descobriremos sua altura:

Vcone=  π • R² • h  
                     3

h= 3 • Vcone  
           πR²

h= 3 • 128 π =  384π  = 6 cm
        π • 8²         64π

h= 6 cm

III)Agora, calcularemos a medida da geratriz deste cone para facilitar o cálculo de sua área.

g²= h² + R²
g²= 6² + 8²
g²= 36 + 64= 100
g= √100
g= 10 cm

IV) Área total do cone:

At= πR² + πRg
At= πR(R + g)
At= 8π(8 + 10)
At= 8 • π • 18
At= 144π cm²

V) Agora, iremos determinar a altura do cilindro desta questão, sabendo que o mesmo possui o mesmo raio e volume do cone mencionado na questão.

R'= 8 cm
Vcilindro= 128π cm³
Vcilindro= π • R'² • h'

h'= Vcilindro  
        π • R'²

h'=  128π   =   128π   = 2 cm
       π • 8²         64π

h'= 2 cm

VI) Agora, calcularemos a área deste cilindro:

At'= 2πR'(R' + h')
At'=2 • π • 8 • (2 + 8)
At'= 160π cm²

VII) Para obtermos a resposta, iremos dividir a área total do cone pela do cilindro.

At/At'= 144π/160π= 9/10
At/At'= 0,9

Resposta: Item c

Desafio 2- (IME 2002)
I) Primeiramente, como a questão diz que o vértice do cone toca a outra base do cilindro e que ambos os sólidos têm uma base comum, podemos afirmar que ambos apresentam a mesma altura e o mesmo raio. Comparando a razão entre suas áreas, teremos:

Acil/Aco=2πr(r + h)/πr(r + g)= 7/4
Acil/Aco= 2(r + h)/(r + g)= 7/4

4 • 2(r + h)= 7(r + g)
8(r + h)= 7r + 7g
8r + 8h= 7r + 7g
8r - 7r = 7g -8h
r= 7g - 8h

II) No triângulo retângulo abaixo, formado neste cone, chamaremos de α o ângulo entre o eixo do cone (que corresponde a altura no centro da base superior do cilindro) e sua geratriz. Nesse triângulo, teremos:

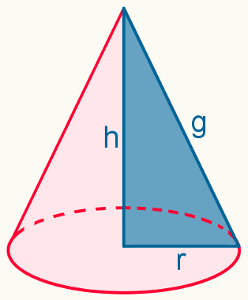
sen α= r/g
cos α= h/g

Então, se dividirmos tudo por g, teremos:

r= 7g - 8h
r/g= 7g/g - 8(h/g)
sen α= 7 - 8 cos α

IV) Elevando os membros da equação ao quadrado teremos:

sen² α= (7 - 8 cos α)²
sen² α= 49 - 112 cos α + 64 cos² α

- Substituindo sen² α= 1 - cos² α e simplificando

1 - cos² α= 49 - 112 cos α + 64 cos² α
65 cos² α - 112 cos α + 48= 0

V) Agora, resolveremos esta equação trigonométrica pela fórmula de Bháskara, mas ela pode ser também resolvida por fatoração:
∆=b² - 4ac
∆=(-112)² - 4 • 65 • 48
∆= 12544 - 12480
∆= 64

cos α= [-(-112)  ± √64]/(2 • 65) =  (112 ± 8)/130
-As raízes desta equação serão:
cos α= (112 + 8)/ 130= 120/130= 12/13
                       ou
cos α= (112 - 8)/130= 104/130= 4/5

VI) Substituiremos as raízes desta equação quadrática na primeira igualdade desenvolvida para conferir as respostas. 
-Primeira raiz:
sen α= 7 - 8 cos α
sen α= 7 - 8 • (12/13)
sen α= 7 - 96/13= (91 - 96)/13
sen α= -5/13 (não serve, pois α < 90°)

-Segunda raiz:
sen α= 7 - 8 cos α
sen α= 7 - 8 • (4/5)
sen α= 7 - 32/5= (35 - 32)/5
sen α= 3/5 

Com isso, temos que o cosseno do ângulo procurado é 4/5. Como o problema pediu o ângulo, podemos escrever:

α= arccos 4/5

Resposta: α= arccos 4/5

Questão 3 - (EFOMM 2011)
Dados:
d= 6√5 m
a + b + c= 22 m
I) Sabendo que a maior distância entre dois vértices de um paralelepípedo corresponde a sua diagonal e conhecendo os dados fornecidos, teremos:
d²= a² + b² + c²
a² + b² + c²= (6√5)²= 180
a² + b² + c²= 180

II) A área total do paralelepípedo é:

At= 2(ab + ac + bc)= (a + b + c)² - (a² + b² + c²)= 22² - 180
At= 2(ab + ac + bc)= 484 - 180= 384
At= 384 m²

-Logo, metade da sua área total será:

At/2= 304/2
At/2= 152 m²

Resposta: Item c

Agradecimentos:

Agradeço a todos que prestigiaram o meu blog e espero que gostem das atuais e futuras postagens. Quem tiver dúvidas, pode comentá-las. Espero ter ajudado.

Referências:

1-https://www.tutorbrasil.com.br/forum/viewtopic.php?f=2&t=73999]
2-http://madematica.blogspot.com/2014/04/exercicios-resolvidos-de-geometria.html