O que são?
O conjunto dos números complexos se trata de um conjunto numérico mais abrangente que o dos números reais. Ele foi criado pelos matemáticos para solucionar equações do segundo e terceiro grau. Nestas tentativas, eles se depararam com equações que envolviam raízes quadradas de números negativos e, nas equações quadráticas, encontraram ∆<0. Por sua vez, tais valores não podem ser expressas nos números reais, mas somente no conjunto dos números complexos.
Por isso, os matemáticos passaram a anotar essas raízes usando a letra "i". A base principal é: i=√-1.
Para tornarmos isso mais claro, resolveremos duas equações do segundo grau cujo ∆ < 0 com a fórmula de Bháskara.
* Utilizando a fórmula de Bháskara, teremos:
∆=b² - 4ac
∆=(-14)² - 4 • 1 • (50)
∆=196 - 200
∆= -4
x= 14 ± √-4
2 • 1
x= 14 ± √-4
2
*Visto que não é possível determinar √-4 no conjunto dos números reais, utilizaremos i=√-1 e teremos que: √-4= √(4 • -1)= 2√-1= 2i. Portanto as soluções dessa equação seriam:
x= 14 ± √-4
2
x= 14 ± 2i
2
x= 7 ± i
x'= 7 + i
x"= 7 - i
V={7 + i, 7 - i}
Esse tipo de número é um número complexo.
Exemplo 2: x² - 6x + 10
* Utilizando a fórmula de Bháskara, teremos:
∆=b² - 4ac
∆=(-6)² - 4 • 1 • (10)
∆=36 - 40
∆= -4
x= 6 ± √-4
2 • 1
x= 6 ± √-4
2
*Visto que não é possível determinar √-4 no conjunto dos números reais, utilizaremos i=√-1 e teremos que: √-4= √(4 • -1)= 2√-1= 2i. Portanto, as soluções dessa equação seriam:
x= 6 ± √-4
2
x= 6 ± 2i
2
x= 3± i
x'= 3 + i
x"= 3 - i
V={3 + i, 3 - i}

cos θ= √3/2 => θ= 30° ou π/6 rad
sen θ= b/|z|
sen θ= 1/2 => θ= 30° ou π/6 rad
cos θ= 1 = 1 • √2 = √2
√2 √2 √2 √2
cos θ= √2/2 => θ= 45° ou π/4 rad
sen θ= b
10-https://www.somatematica.com.br/emedio/complexos/complexos2.php
11-https://mundoeducacao.bol.uol.com.br/matematica/forma-trigonometrica-ou-polar-um-numero-complexo.htm
Por isso, os matemáticos passaram a anotar essas raízes usando a letra "i". A base principal é: i=√-1.
Para tornarmos isso mais claro, resolveremos duas equações do segundo grau cujo ∆ < 0 com a fórmula de Bháskara.
Exemplificações:
Exemplo 1: x² - 14x + 50= 0* Utilizando a fórmula de Bháskara, teremos:
∆=b² - 4ac
∆=(-14)² - 4 • 1 • (50)
∆=196 - 200
∆= -4
x= 14 ± √-4
2 • 1
x= 14 ± √-4
2
*Visto que não é possível determinar √-4 no conjunto dos números reais, utilizaremos i=√-1 e teremos que: √-4= √(4 • -1)= 2√-1= 2i. Portanto as soluções dessa equação seriam:
x= 14 ± √-4
2
x= 14 ± 2i
2
x= 7 ± i
x'= 7 + i
x"= 7 - i
V={7 + i, 7 - i}
Esse tipo de número é um número complexo.
Exemplo 2: x² - 6x + 10
* Utilizando a fórmula de Bháskara, teremos:
∆=b² - 4ac
∆=(-6)² - 4 • 1 • (10)
∆=36 - 40
∆= -4
x= 6 ± √-4
2 • 1
x= 6 ± √-4
2
*Visto que não é possível determinar √-4 no conjunto dos números reais, utilizaremos i=√-1 e teremos que: √-4= √(4 • -1)= 2√-1= 2i. Portanto, as soluções dessa equação seriam:
x= 6 ± √-4
2
x= 6 ± 2i
2
x= 3± i
x'= 3 + i
x"= 3 - i
Forma algébrica:
Um número complexo pode ser escrito de duas formas: Uma polar e outra algébrica. Falaremos somente sobre esta última.
A forma algébrica de um número complexo é escrita como:
z= a + bi, com a,b ∈ IR
Onde:
z=> número complexo
a=> Parte real de z
b=> Parte imaginária de z
i=√-1
z=> número complexo
a=> Parte real de z
b=> Parte imaginária de z
i=√-1
Exemplos:
z1= 3 + 5i
Onde:
a=3 (parte real)
b= 5 (parte imaginária)
z1= 2 + 7i
Onde:
a=2 (parte real)
b= 7 (parte imaginária)
Representação gráfica:
Os números complexos podem ser representados em um plano similar ao plano cartesiano conhecido como plano Argand-Gauss. Nele, o eixo das ordenadas (ou eixo y) representa a parte imaginária do número complexo e o eixo das abscissas (ou eixo x) representa a sua parte real.
Logo abaixo, temos alguns exemplos:
a) Z1= 4 + 6i
b) Z2= -3 - i
c)Z3= -2 + 4i
d)Z4= 5i
e)Z5= 5 - 2i

Conjugado de um número complexo:
O conjugado de um número complexo é um conceito análogo ao conceito do oposto de um número real (exemplo: 2 e -2). Ele é indicado por z é definido como z= a - bi. Assim, trocamos o sinal da parte imaginária.
Portanto:
Se z= a + bi, então z= a - bi
Exemplo: Determine o conjugado de z= 2 + 3i
* Sabendo que z= 2 + 3i, então o seu conjugado será:
z= 2 - 3i
Quando multiplicamos um número complexo por seu conjugado
Operações entre números complexos:
Assim como no conjunto dos números reais, é possível realizar operações de adição, subtração, multiplicação e divisão nos números complexos. Confira as definições e exemplos:
-Soma: A soma de números complexos é realizada através da adição de termos semelhantes. Ou seja, devemos somar as partes reais de cada número e, depois, as imaginárias.
Na forma algébrica, temos:
z'= a + bi
z"= c + di
z' + z"= a + bi + c + di
z' + z"= a + c + (b + d)i
Exemplo:
z'= 5 + 7i
z"= -3 + 4i
z' + z"= a + bi + c + di
z' + z"=(5 + 7i) + (-3 + 4i)
z' + z"= 5 + (-3) + (7 + 4)i
z' + z"= 5 - 3 + 11i
z' + z"= 2 + 11i
-Subtração: A subtração de números complexos é realizada através de um raciocínio análogo da adição, ou seja, devemos subtrair a parte real e, depois, a imaginária.
Na forma algébrica, temos:
z'= a - bi
z"= c - di
z' - z"= (a + bi) - (c + di)
z' - z"= a - c + (b - d)i
Exemplo:
z'= 4 - 5i
z"= 2 + i
z' - z"= (a + bi) - (c + di)
z' - z"=(4 - 5i) - (2 + i)
z' - z"= 4 - 2 + (-5 - 1)i
z' - z"= 2 - 6i
Multiplicação: Para realizarmos a multiplicação entre números complexos, devemos utilizar a propriedade distributiva da multiplicação.
Dado dois números complexos z'= a + bi e z"= c + di, o produto deles será
z' • z"= (a + bi) • (c + di)
z' • z"= ac +adi + bci + bdi² (i²= -1)
z' • z"= ac + adi + bci - bd
z' • z"= (ac - bd) + (ad + bc)i
Exemplo:
z'= 4 - 3i
z"= 6 + 5i
z' • z"= (a + bi) • (c + di)
z' • z"= (4 - 3i) • (6 + 5i)
z' • z"= 4 • 6 +4 • 5i + (-3i) • 6 +(-3i) • 5i (i²= -1)
z' • z"= 24 + 20i - 18i - 15i² (i²= -1)
z' • z"= 24 + 2i + 15
z' • z"= 2i + 39
Divisão: Para dividirmos números complexos, devemos multiplicar a divisão pelo conjugado do denominador. Considerando dois números complexos z'= a + bi e z"= c + di, o quociente deles será:
z' = a + bi
z" c + di
z' = a + bi • (c - di)
z" c + di (c - di)
z' = ac - adi + bci - bdi²
z" c² - (di)²
z' = ac + bd + (bc - ad)i
z" c² - (di)²
Exemplo:
z'= 1 + 2i
z"= 2 + 3i
z' = 1 + 2i • (2 - 3i)
z" 2 + 3i (2 - 3i)
z' = 1 + 2i • (2 - 3i)
z" 2² - (3i)²
z' = 8 - i
z" 4 + 9
z' = 8 - i
z" 13
Forma trigonométrica ou polar de um número complexo:
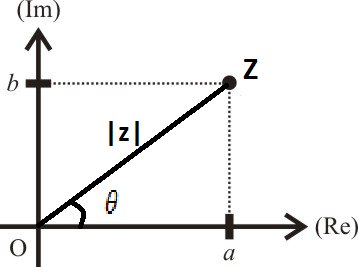
Como visto anteriormente, um número complexo pode ser representando num plano de dois eixos perpendiculares conhecido como plano Argand-Gauss. O segmento horizontal apresenta a parte real de um número complexo e o eixo vertical, a parte imaginária. Considere um número complexo
z= a + bi representado neste plano.

O segmento OZ é conhecido como módulo do número complexo e é representado por |z|. O ângulo entre o eixo Ox e o segmento OZ é conhecido como argumento, representado por θ.
A partir do triângulo OâZ formado, teremos que:
|z|²= a² + b²
|z|= √(a² + b²)
cos θ= a/|z|
a= |z| • cos θ
sen θ= b/|z|
b= |z| • sen θ
Lembrando- se que um número complexo é escrito na forma z= a + bi, teremos:
A partir do triângulo OâZ formado, teremos que:
|z|²= a² + b²
|z|= √(a² + b²)
cos θ= a/|z|
a= |z| • cos θ
sen θ= b/|z|
b= |z| • sen θ
Lembrando- se que um número complexo é escrito na forma z= a + bi, teremos:
z= a + bi
z= |z| • cos θ + |z| • sen θ • i
z= |z| • ( cos θ + i • sen θ)
Exemplo 1: Escreva o número complexo z= √3 + i na fórmula trigonométrica.
* Primeiramente,temos que a= √3, b=1. Logo, teremos:
|z|= √(a² + b²)
|z|= √((√3)² + 1²)
|z|= √(3 + 1)
|z|= √4
|z|= 2
Procede-se que:
cos θ= a/|z|
cos θ= a/|z|
cos θ= √3/2 => θ= 30° ou π/6 rad
sen θ= b/|z|
sen θ= 1/2 => θ= 30° ou π/6 rad
Assim, a fórmula trigonométrica deste número é:
z= |z| • ( cos θ + i • sen θ)
z= 2 • ( cos 30° + i • sen 30°)
z= 2 • ( cos π/6 + i • sen π/6)
Exemplo 2:Escreva o número complexo z= 1 + i na fórmula trigonométrica.
* Primeiramente,temos que a= 1, b=1. Logo, teremos:
|z|= √(a² + b²)
|z|= √(1² + 1²)
|z|= √(1 + 1)
|z|= √2
Procede-se que:
cos θ= a
|z|
cos θ= a
|z|
√2 √2 √2 √2
cos θ= √2/2 => θ= 45° ou π/4 rad
sen θ= b
|z|
sen θ= 1 = 1 • √2 = √2
√2 √2 √2 √2
sen θ= √2/2 => θ= 45° ou π/4 rad
sen θ= 1 = 1 • √2 = √2
√2 √2 √2 √2
sen θ= √2/2 => θ= 45° ou π/4 rad
Assim, a fórmula trigonométrica deste número é:
z= |z| • ( cos θ + i • sen θ)
z= 2 • ( cos 45° + i • sen 45°)
z= 2 • ( cos π/4 + i • sen π/4)
Exemplo 3:Escreva o número complexo z= 8i na fórmula trigonométrica.
* Primeiramente,temos que a= 0, b=8. Logo, teremos:
|z|= √(a² + b²)
|z|= √(0² + 8²)
|z|= √(0 + 64)
|z|= √64
|z|= 8
Procede-se que:
cos θ= a
|z|
cos θ= 0 = 0 => θ= 90° ou π/2 rad
8
sen θ= b
|z|
sen θ= 8 = 1
8
sen θ= 1 => θ= 90° ou π/2 rad
Assim, a fórmula trigonométrica deste número é:
z= |z| • ( cos θ + i • sen θ)
z= 8 • ( cos 90° + i • sen 90°)
z= 8 • ( cos π/2 + i • sen π/2)
Agradecimentos:
Agradeço a todos que prestigiaram o meu blog e espero que gostem das atuais e futuras postagens. Quem tiver dúvidas, pode comentá-las. Espero ter ajudado.
Referências:
5-https://www.colegioweb.com.br/numeros-complexos/representacao-geometrica-dos-numeros-complexos.html
7-http://matnumeroscomplexos.blogspot.com/2014/04/conhecendo-o-plano-de-argand-gauss.html
8-https://www.paratodosesobretudo.com.br/2011/02/resolva-equacoes-de-2-grau-com-raizes.html
9-https://www.todamateria.com.br/numeros-complexos/8-https://www.paratodosesobretudo.com.br/2011/02/resolva-equacoes-de-2-grau-com-raizes.html
10-https://www.somatematica.com.br/emedio/complexos/complexos2.php
11-https://mundoeducacao.bol.uol.com.br/matematica/forma-trigonometrica-ou-polar-um-numero-complexo.htm
Nenhum comentário:
Postar um comentário