Queda livre e lançamento vertical

O que é?

Movimento de queda livre é o movimento de lançamento vertical que ocorre próximo à superfície da Terra ao abandonar corpos de massa m no vácuo ou em locais onde se despreza a resistência do ar.
Este movimento é uniformemente variado, sua aceleração é constante e possui módulo igual a
g= 9,8 m/s^2. Na maioria dos casos, aceita-se a aproximação do valor para 10 m/s^2.
Durante a queda de um corpo, sua velocidade aumenta porque o sinal da aceleração gravitacional da Terra é positivo.
Neste movimento, a velocidade inicial da partícula (Vo) é nula pelo fato de ele ser somente abandonado à ação da gravidade.
Agora serão apresentadas as equações da queda livre:

*Equação horária do espaço da queda livre:

h= gt²
2

Onde:
g- aceleração gravitacional da Terra (10 m/s^2)
h- Altura (m)
t- Tempo de queda (s)

Exemplo: Em um edifício de construção, um tijolo cai acidentalmente em uma altura de 45 m. Determine o tempo de queda deste tijolo.

I) Ao lermos o problema com atenção, podemos perceber que o corpo em questão se encontra em queda livre e que o problema nos dá as seguintes informações:

h= 45 m

g= 10 m/s²

II) Substituindo estes dados na equação horária da queda livre, descobrimos que a altura do prédio será:

h= gt²

45= 10 • t²

5t²= 45

t²= 45

t²= 9

t= √9

t= 3 s

Resposta: O tijolo demora 3 s para cair deste prédio.

*Equação horária da velocidade da queda livre:
V= Vo + gt
- Como Vo= 0, temos que:
V=gt
Onde:
g- aceleração gravitacional da Terra (10 m/s^2)
t- Tempo de queda (s)

Exemplo: Em um edifício de construção, um tijolo cai acidentalmente e chega solo 3 segundos depois. Determine a velocidade com a qual ele cai deste prédio

I) Ao lermos o problema com atenção, podemos perceber que o corpo em questão se encontra em queda livre e que o problema nos dá as seguintes informações:

t= 3 s

g= 10 m/s²

II)Agora, utilizaremos a equação horária da velocidade da queda livre para determiná-la.

V=gt

V= 10 • 3

V= 30 m/s

Resposta: A velocidade com a qual eeste tijolo cai deste prédio é igual a 30 m/s.

*Equação de Torriceli da queda livre:

V²= Vo²+ 2g∆h
- Como Vo= 0, temos que:
V²=2g∆h
V=√2g∆h

Onde:
g- aceleração gravitacional da Terra (10 m/s²)
∆h- Variação de altura (m)
V= velocidade de queda (m/s)

*Obs: Quando o tema de conservação de energia for abordado, a dedução desta equação será demonstrada.

Exemplo: Uma esfera de massa de 3 kg é solta do alto de um prédio, cuja altura é 20 m. Calcule a velocidade dessa esfera quando ela atinge o chão, considerando a aceleração da gravidade g=10 m/s^2.

I) Ao analisarmos o problema, podemos observar que ele nos forneceu as seguintes informações:
h= 40 m
g= 10 m/s²
Vo= 0

II) A velocidade desta esfera será dada ao substituirmos a altura e aceleração da questão na fórmula:
V= √2g∆h
V=√2 • 10 • 20
V= √400
V=20 m/s

Resposta: V= 20 m/s

Lançamento vertical:

Quando lançamos um corpo para cima ou para baixo com uma certa velocidade inicial, denominamos este movimento como lançamento vertical. Este movimento também é um movimento uniformemente variado M.U.V, assim como a queda livre. A aceleração do lançamento vertical é a aceleração gravitacional da Terra.

Existem duas classificações para este tipo de movimento:

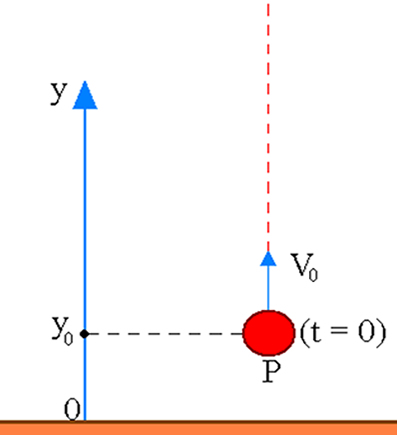
Lançamento vertical para cima:

À medida que um corpo sobe, sua velocidade diminui até que se anule no ponto de altura máxima. Isso ocorre pelo fato deste movimento ser retardado, ou seja, ele se opõe a ação da gravidade.

Fonte:https://mundoeducacao.bol.uol.com.br/fisica/lancamento-vertical-para-cima.htm

Lançamento vertical para baixo:

Ao contrário do que se observa no lançamento vertical para cima, a situação estudada anteriormente, o lançamento vertical para baixo é um movimento acelerado porque ele não se opõe a ação da gravidade, sendo favorecido por ela.

Fonte:https://mundoeducacao.bol.uol.com.br/fisica/movimento-queda-livre-lancamento-vertical.htm

Fórmulas do lançamento vertical:

* Equação horária do lançamento vertical:

h=ho + Vo t ± gt²
2
* Equação horária da velocidade do lançamento vertical

V= Vo ± gt

*Equação de Torriceli para o lançamento vertical:

V²= Vo² ± 2g (h - ho)
V²= Vo² ± 2g∆h

No lançamento vertical para cima, a aceleração é positiva (g > 0). Enquanto no lançamento vertical para cima, a aceleração é negativa (g < 0).

Exercícios:

Questão 1) Um objeto é abandonado do alto de um prédio e inicia uma queda livre. Sabendo que esse objeto leva 3 s para atingir o chão, calcule a altura desse prédio, considerando a aceleração da gravidade igual a 10 m/s².

Questão 2) (PUC- RIO 2009) - Um objeto é lançado verticalmente para cima, de uma base, com velocidade V= 30 m/s. Indique a distância percorrida pelo objeto desde sua saída da base até seu retorno, considerando a aceleração da gravidade g= 10 m/s².
a) 30 m;
b) 55 m;
c) 70 m;
d) 90 m;
e) 100 m;

Questão 3) Um corpo é abandonado a 80 m do solo. Sendo g= 10 m/s² e o corpo estando livre de forças dissipativas, determine o instante e a velocidade que o móvel possui ao atingir o solo.

Questão 4) (PUC- RIO 2008) Uma bola é lançada verticalmente para cima, a partir do solo, e atinge uma altura de 20 m. Considerando a aceleração da gravidade g= 10 m/s², a velocidade inicial de lançamento e o tempo de subida da bola são:
a) 10 m/s e 1 s;
b) 20 m/s e 2 s;
c) 30 m/s e 3 s;
d) 40 m/s e 4 s;
e) 50 m/s e 5 s;

Questão 5) (PUC- RIO 2008)- Em um campeonato recente de vôo de precisão, os pilotos de avião deveriam “atirar” um saco de areia dentro de um alvo localizado no solo. Supondo que o avião voe horizontalmente a 500 m de altitude com uma velocidade de 144 km/h, e que o saco é deixado cair do avião, ou seja, no instante do “tiro” a componente vertical do vetor velocidade é zero, podemos afirmar que: (Considere a aceleração da gravidade g = 10m/s² e despreze a resistência do ar)

a) O saco deve ser lançado quando o avião se encontra a 100 m do alvo;
b) O saco deve ser lançado quando o avião se encontra a 200 m do alvo;
c) O saco deve ser lançado quando o avião se encontra a 300 m do alvo;

d) O saco deve ser lançado quando o avião se encontra a 400 m do alvo;

e) O saco deve ser lançado quando o avião se encontra a 500 m do alvo;

Resoluções:

Questão 1)

I) Ao lermos o problema com atenção, podemos perceber que o corpo em questão se encontra em queda livre e que o problema nos dá as seguintes informações:

t= 3 s

g= 10 m/s²

II) Substituindo estes dados na equação horária da queda livre, descobrimos que a altura do prédio será:

h= gt²

h= 10 • 3²

h= 10 • 9

h= 90

h= 45 m

Resposta: A altura do prédio mede 45 m

Questão 2)

I) Ao lermos o problema com atenção, podemos perceber que o corpo em questão se encontra em um lançamento vertical para cima e que o problema nos dá as seguintes informações:

V= 0 ( Velocidade no ponto mais alto do lançamento)

Vo= 30 m/s

g= -10 m/s² (esta aceleração é negativa porque o movimento é retardado)

∆h= ?

II) Substituindo os dados na fórmula da equação de Torriceli do lançamento vertical, temos que a altura de subida do objeto será:

V²= Vo² - 2g∆h

0²= 30² - 2 • 10 • ∆h

0= 900 - 20∆h

20∆h= 900

∆h= 900

∆h= 45 m

III) Como a distância percorrida pelo objeto em sua subida e descida corresponde ao dobro de sua altura máxima, podemos dizer que esta distância será:

H=2∆h

H= 2 • 45

H= 90 m

Resposta: Item d

Questão 3)

I) Ao lermos o problema com atenção, podemos perceber que o corpo em questão se encontra em queda livre e que o problema nos dá as seguintes informações:

h= 80 m

g= 10 m/s²

II) Substituindo estes dados na equação horária da queda livre, descobrimos que a altura do prédio será:

h= gt²

80= 10 • t²

5t²= 80

t²= 80

t²= 16

t= √16

t= 4 s

III) Como o problema também quer a velocidade de queda deste objeto, utilizaremos a equação horária da velocidade da queda livre para determiná-la.

V=gt

V= 10 • 4

V= 40 m/s

Resposta: t= 4s e V= 40 m/s

Questão 4)

I) Ao lermos o problema com atenção, podemos perceber que o corpo em questão se encontra em um lançamento vertical para cima e que o problema nos dá as seguintes informações:

V= 0 ( Velocidade no ponto mais alto do lançamento)

Vo= ?

g= -10 m/s²

∆h= 20 m

II) Substituindo os dados na fórmula da equação de Torriceli do lançamento vertical, temos que a altura de subida do objeto será:

V²= Vo²- 2g∆h

0²= Vo² - 2 • 10 • 20

0=Vo² - 400

Vo²= 400

Vo=√400

Vo= 20 m/s

III) Como o problema também quer o tempo de queda deste objeto, utilizaremos a equação horária da velocidade do lançamento vertical para determiná-la.

V=Vo - gt

0= 20 - 10t

10t= 20

t= 20

t= 2 s

Resposta: Item b.

Questão 5)

I) Ao lermos o problema detalhadamente, podemos perceber que o corpo em questão se encontra em um lançamento horizontal e que o problema nos dá as seguintes informações:

V= 144 km/h= 40 m/s (M.U)

h= 500 m

g= 10 m/s²

II) Agora, utilizaremos a equação da queda livre para determinar o tempo de queda do saco:

h= gt²

500= 10 • t²

500= 5t²

5t²= 500

t²= 500

t²= 100

t= √100

t= 10 s

III) Quando o saco é deixado para cair no alvo, sua velocidade horizontal é constante e possui intensidade de 40 m/s. Logo o seu deslocamento será:

S= So + Vt

S= 0 + 40 • 10

S= 400 m

Resposta: Item d.

Agradecimentos:

Agradeço a todos que prestigiaram o meu blog e espero que gostem das atuais e futuras postagens. Quem tiver dúvidas, pode comentá-las. Espero ter ajudado.