Física- Movimento Retilíneo Uniformemente Variado (M.R.U.V)

O que é?

O movimento retilíneo uniformemente variado (M.R.U.V) é o movimento descrito por corpos cujo velocidade varia uniformemente em razão do tempo. Por isso, ele pode ser definido como qualquer movimento no qual a aceleração é constante. A velocidade de uma partícula em M.R.U.V sempre sofrerá variações de velocidade em intervalos iguais de tempo.

Este tipo de movimento pode ser uma trajetória horizontal ou vertical e ele ocorre em diversas situações do cotidiano, tais como a freada de um carro ou o lançamento de um foguete ao espaço.

Movimento retilíneo uniformemente acelerado:

Movimento retilíneo uniformemente acelerado é o movimento no qual a velocidade inicial do corpo Vo é menor que a velocidade V do mesmo ( V> Vo) , ou seja, este é o movimento no qual o módulo da velocidade do móvel aumentará pelo fato da aceleração escalar ser maior que zero (a > 0).
Este tipo de movimento pode ser progressivo, quando Vo > 0, ou retrógrado, quando Vo < 0.

Movimento retilíneo uniformemente retardado:

Movimento retilíneo uniformemente acelerado é o movimento no qual a velocidade inicial do corpo Vo é maior que a velocidade V do mesmo ( V< Vo) , ou seja, este é o movimento no qual o módulo da velocidade do móvel diminuirá pelo fato da aceleração escalar ser menor que zero (a < 0).
Este tipo de movimento pode ser progressivo, quando Vo > 0, ou retrógrado, quando Vo < 0.

Função horária da velocidade:

Esta função indica a relação entre a velocidade e o tempo. Para determinamos esta função, deve-se lembrar o conceito de aceleração média.

am= ∆V

∆t

Ao isolarmos ∆V, temos que:

∆V= a • ∆t

V - Vo= a • ∆t
V= Vo + a • ∆t

Considerando To= 0, a função horária da velocidade será escrita como:

V= Vo + at

O gráfico desta função será uma reta por ser uma função do primeiro grau

Exemplo: A velocidade de uma partícula varia de acordo com a função V= 4 + 8t Pede-se:
a) Velocidade inicial da partícula
b) A aceleração da partícula
c) A velocidade da partícula no instante t= 2 s
d) A variação de velocidade nos 4 primeiros segundos

* Obs: Sempre leia os problemas com cuidado para utilizar os dados corretamente e resolver o problema.

Resolução:
Item a)
I) Como V= V0 + at e temos V= 4 + 8t.
V0= 4 m/s

Resposta: V0= 4 m/s

Item b) Como V= V0 + at e temos V= 4 + 8t.
a= 8 m/s^2

Resposta: a= 8 m/s^2

Item c) No instante t= 2 s, a velocidade da partícula será:
V= 4 + 8t
V= 4 + 8 • 2
V= 4 + 16
V= 20 m/s

Resposta: V= 20 m/s

Item d)
I) Como conhecemos a velocidade inicial do móvel, devemos calcular a velocidade do móvel após 4 s.
V4= 4 + 8 • 4
V4= 4 + 32
V4= 36 m/s

II) A variação de velocidade deste móvel corresponderá a diferença entre a velocidade final e inicial do móvel. Logo, ela será igual a:

∆V= V4 - Vo
∆V= 36 - 4
∆V= 32 m/s

Resposta: ∆V= 32 m/s

Função horária do espaço:

Resultado de imagem para função da velocidade em relação ao tempo

Fonte:https://www.sofisica.com.br/conteudos/Mecanica/Cinematica/muv.php

Ao observamos o gráfico da função horária da velocidade acima, podemos perceber que a área deste gráfico corresponde ao deslocamento da partícula e a área de um trapézio. Com isso, podemos dizer que a área deste corpo será igual:

∆S= V + Vo • t

Lembremos também que:

V= Vo + at

Logo:

∆S= Vo + at + Vo • t

∆S= 2Vot + at²

2 2

∆S= Vot + at²

S - So= Vot + at²

S= So + Vot + at²

A fórmula acima representa uma função do segundo grau que apresenta um gráfico cujo desenho é uma parábola, tal como o gráfico que se encontra na imagem abaixo.

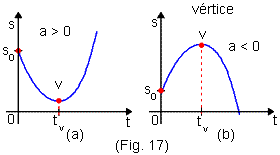
Resultado de imagem para grafico espaço em função do tempo

Fonte:https://www.10emtudo.com.br/login
Gráfico do espaço percorrido por um corpo no M.R.U.V em função do tempo

Exemplo: Suponhamos que a velocidade de um automóvel com velocidade inicial de 10 m/s, acelere a 1 m/s^2 constantemente. A distância percorrida nos seis primeiros segundos será igual a:

* Obs: Sempre leia os problemas com cuidado para utilizar os dados corretamente e resolver o problema.

Resolução:
I) Ao ler o problema, pode-se perceber que ele forneceu as seguintes informações:
Aceleração- a= 1 m/s^2
Velocidade inicial - Vo= 10 m/s
So= 0 m
S=?

II) Agora, basta aplicar a função horária do espaço para determinar a distância percorrida por este móvel:

S= So + Vot + at²
2

S= 0 + 10 • 6 + 1 • 6²
2
S= 60 + 36
2

S= 60 + 18

S= 78 m

Resposta: o espaço percorrido por este móvel nos seis primeiros segundos foi de 78 metros.

Equação de Torriceli:

Até agora, trabalhamos equações que determinam a velocidade ou deslocamento do M.R.U.V apenas em função do tempo.

Seria muito melhor se conhecêssemos uma equação na qual seja possível determinar a velocidade de um móvel sem que o tempo seja conhecido.
Tal equação existe, ela é conhecida como equação de Torriceli e é escrita como:

V²= Vo²+ 2a∆S

Onde:
V = velocidade final (m/s)
∆S = deslocamento (m)
a = aceleração (m/s^2)
Vo =Velocidade inicial (m/s)

Obs: Como esta equação possui uma dedução muito longa, não irei deduzi-lá.

Exemplo: Um carro parte do repouso com uma aceleração escalar constante de 2,0 m/s^2 e percorre 25 m. Qual a velocidade final atingida pelo carro?

* Obs: Sempre leia os problemas com cuidado para utilizar os dados corretamente e resolver o problema.

Resolução:
I) Ao ler o problema, pode-se perceber que ele forneceu as seguintes informações:
Aceleração- a= 2 m/s^2
Velocidade inicial - Vo= 0 m/s (repouso)
Deslocamento- ∆S= 25 m
Velocidade final- V= ?

II) Nota-se na análise dos dados a ausência da grandeza tempo. Portanto, a velocidade final deste carro será dada pela equação de Torriceli

V²= Vo²+ 2a∆S
V²= 0² + 2 • 2 • 25
V²= 100
V= √100
V= 10 m/s

Resposta: O carro atinge uma velocidade final igual a 10 m/s.

Dominando o conhecimento - Exercícios:

Questão 1) (Fuvest) Um veículo parte do repouso em movimento retilíneo e acelera com aceleração escalar constante e igual 2 m/s^2. Pode-se dizer que sua velocidade escalar e a distância percorrida após 3,0 segundos, valem, respectivamente:

a) 6 m/s e 9 m

b) 6 m/s e 18 m

c) 3 m/s e 12 m

d) 12 m/s e 35 m

Questão 2) (CFT - MG) O movimento de um corpo é descrito pela equação v= 10 - 2t em que v é a velocidade, em m/s, e t é o tempo em segundos.

Durante os primeiros 5,0 s, a distância percorrida por ele, em metros, será:

a) 10

b) 15

c) 20

d) 25

Questão 3) Um anúncio de um certo tipo de automóvel proclama que o veículo, partindo do repouso, atinge a velocidade de 180 km/h em 8 s. Qual é a aceleração média desse automóvel?

Questão 4) ( Mack- SP) Uma partícula inicialmente em repouso passa a ser acelerada constantemente à razão de 3 m/s^2 no sentido da trajetória. Após ter percorrido 24 m, sua velocidade é:

a) 3,0 m/s

b) 8,0 m/s

c) 12,0 m/s

d) 72,0 m/s

e)144 m/s

Questão 5) A velocidade escalar de um trem reduz uniformemente de 12 m/s para 6 m/s. Sabendo-se que, durante esse tempo, o trem percorre 100 m, qual o módulo de sua desaceleração?

Questão 6) Um móvel parte do repouso e com aceleração constante de 5 m/s^2 atinge a velocidade de 20 m/s. Determine a variação do espaço do móvel enquanto sua velocidade variava.

Questão 7) Considere dois móveis que, sobre uma mesma trajetória, realizam movimentos que obedecem as funções horárias s1= -2 + 6t e s2= 4- 3t + 3t^2 ( s em metros e t em segundos)

a) Em que instante(s) os móveis se cruzam?

b) Em que posição (ou posições) os móveis se cruzam?

Questão 8) Certo móvel, inicialmente na velocidade de 3 m/s, acelera constantemente a 2 m/s^2 até se distanciar 4 m de sua posição inicial. O intervalo de tempo decorrido até o término desse deslocamento foi:

a) 4,0 s

b) 1,0 s

c) 3,0 s

d) 5,0 s

e) 2,5 s

Resoluções:

Questão 1)
I) Ao analisarmos a situação, podemos concluir que a função horária da velocidade deste móvel será:

V=V0 + at

V0= 0
a= 2 m/s^2

V= 2t

II) Para t= 3 s, a velocidade do móvel será:

V=2 • 3
V= 6 m/s

III) Como o problema também deseja saber o deslocamento deste corpo, aplicaremos a equação horária do espaço para determinarmos isso.

S= So + Vot  + at²
2
* Como So=0 e Vo= 0 teremos o deslocamento escrito apenas como:

S=  at^2
2

S= 2 • 3^2
2
S= 2 • 9
2

S= 9 m

Resposta: Item a.

Questão 2)
I) Primeiramente, devemos analisar os termos desta função horária
v= vo + at
v= 10 - 2t

vo= 10 m/s
a= -2 m/s^2

II) Visto que a velocidade inicial e a aceleração deste móvel são conhecidos, podemos calcular o espaço percorrido por este móvel no instante t= 5 s através da equação horaria do espaço escrita como:

∆S= Vot  + at^2
2

∆S= 10 • 5 + (-2) • 5²
2
∆S= 50 + (-2) • 25
2
∆S= 50 - 25

∆S= 25 m

Resposta: Item d

Questão 3)
I) Ao analisarmos o problema, podemos perceber que ele nos fornece as seguintes informações:
Vo= 0 m/s
V= 180 km/h= 50 m/s
∆t= 8 s

II) A aceleração deste carro será dada por:

a=  V - Vo
∆t

a= 50 - 0
8

a= 50 m/s
8 s

a= 6,25 m/s^2

Resposta: a= 6,25 m/s^2

Questão 4)

I) Ao analisarmos os dados que o problema dá, podemos dizer que:

V= ?

Vo= 0 m/s
a= 3 m/s^2

V²= 0 + 144

V²= 144

V=√144
V= 12 m/s

Resposta: Item c

Questão 5)

I) Ao analisarmos os dados que o problema dá, podemos dizer que:

V= 6 m/s

Vo= 12m/s
∆S=100 m
a=?

II) Para calcularmos a desaceleração do trem, aplicaremos a equação de Torriceli

V²= Vo² + 2a∆S

6²= 12² + 2 • a • 100

36= 144 + 200a

-200a= 144 - 36

-200a= 108

a= - 108

200

a= -0,54 m/s²

|a|= 0,54 m/s² (módulo da desaceleração)

Resposta: |a|= 0,54 m/s^2.

Questão 6)

I) Ao analisarmos os dados que o problema dá, podemos dizer que:

V= 10 m/s

Vo=0 m/s
a= 5 m/s²

∆S= ?

II) Aplicaremos a equação de Torriceli para determinarmos o deslocamento, variação de espaço, deste móvel.

V²= Vo² + 2a∆S

20²= 0² + 2 • 5 • ∆S

400= 10∆S

400 = ∆S

∆S= 40 m

Resposta: ∆S= 40 m

Questão 7)
Questão 7- item a)
I) Como os móveis se cruzam no mesmo instante, podemos igualar as duas equações e o instante de encontro entre os dois móveis será dado pela seguinte igualdade:

s2=s1
4- 3t + 3t²= -2 + 6t
3t² - 3t + 4= 6t -2
3t² - 3t - 6t + 4 + 2= 0
3t² - 9t + 6= 0

* Dividindo ambos os lados da equação por 3

t² - 3t + 2= 0

II) Como a equação acima é do segundo grau aplicaremos a fórmula de Bhaskara.
∆=b² - 4ac
∆= (-3)² - 4 • 1 • (-2)
∆= 9 - 8
∆= 1

t= 3 ± √1
2 • 1
t= 3 ± 1
2

t'= 3 + 1
2

t'= 2 s

t"= 3 - 1
2

t"= 1 s

Resposta: t'=2 s; t"= 1 s

Questão 7- item b)
I) As posições nas quais estes móveis se cruzam serão determinadas quando substituirmos os valores de t em uma das equações:

Para t= 2 s
s1= -2 + 6t
s1= -2 + 6 • 2
s1= -2 + 12
s1= 10 m

Para t= 1 s
s2= -2 + 6t
s2= -2 + 6 • 1
s2= -2 + 6
s2= 4 m

Resposta: s1= 10m; s2= 4m

Questão 8)
I) A função horária de um móvel cuja aceleração é constante é dada por:

S= So + Vot + at²
2

Substituindo os dados do problema na fórmula da função horária:
Dados:
Aceleração- a= 2m/s²
Velocidade inicial - Vo= 3m/s
So= 0 m
S= 4 m

4= 0 + 3 • t + 2 • t²
2
4=3t + t²

4=t² + 3t
t² + 3t - 4= 0

II) O intervalo de tempo de tempo decorrido até o término deste deslocamento será dado pela fórmula de Bhaskara

∆=b² - 4ac

∆=3^2 - 4 • 1 • (-4)

∆= 9 + 16

∆= 25

t= -3 ± √25

2 • 1

t= -3 ± 5

t'= -3 + 5

t'= 2

t'= 1 s

t"= -3 - 5

t"= - 8

t"= - 4 s (não existe tempo negativo)

Resposta: t= 1 s - Item b.

Agradecimentos:

Agradeço a todos que prestigiaram o meu blog e espero que gostem das atuais e futuras postagens. Quem tiver dúvidas, pode comentá-las. Espero ter ajudado.