Introdução:
A geometria espacial é um ramo da matemática que foca no estudo das figuras tridimensionais, ou seja, aquelas que apresentam largura, comprimento e altura. Ela estuda sólidos geométricos como o cubo, cilindro, cone, prisma e a esfera.
O volume destes objetos é obtida através, essencialmente, de fórmulas específicas para cada sólido.
Apresentaremos algumas fórmulas para o cálculo da volume de alguns sólidos geométricos e como aplicá-las.
Cubo:
É um sólido geométrico que possui arestas e faces congruentes. Ou seja, ele possui medidas iguais de altura, largura e comprimento. Ele é constituído por 8 vértices e 12 arestas
A fórmula para calcular seu volume é dada por:
Cubo cujo arestas medem a.
V=a³
Exemplo I) Qual o volume de um cubo cuja medida da aresta é igual a 4 cm?
I) Como conhecemos a medida do cubo, basta substituí-la na fórmula
V= a³
V= 4³
V= 64 cm³
Paralelepípedo:
Figura tridimensional constituída de 12 arestas e 8 vértices que é definida como um prisma cuja as faces são paralelogramos. O seu volume é dado por:
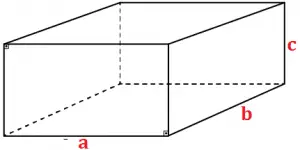
Paraleleppedo com arestas cujas medidas são a,b e c.
V=abc
Exemplo: Calcule o volume de um paralelepípedo que apresenta medidas iguais a 10 cm, 7 cm e 3 cm.
I) Como conhecemos as medidas do paralelepípedo em questão, determinamos o seu volume substituindo estes valores na fórmula.
V= 10 • 7 • 3
V= 210 cm³
Cilindro:
Como fora explicado em postagens anteriores, o cilindro é uma figura geométrica com formato circular que apresenta o mesmo diâmetro em todo o seu comprimento. Ele é composto por duas bases circulares dispostas em planos distintos e perpendiculares e todos os pontos entre eles.
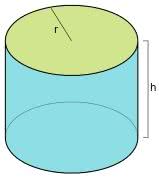
Raio: Distância entre o centro e uma extremidade do cilindro. (r)
Base: O cilindro apresenta uma base superior e inferior. Ambas são circulares, paralelas entre si e congruentes.
Geratriz: Segmento que passa de uma base para a outra. Corresponde a altura do cilindro.(altura h=g)
Diretriz: Corresponde aos pontos da geratriz nas extremidades do cilindro.
O seu volume é dado pela seguinte fórmula:
V= π r²h
Exemplo: Dado um cilindro de raio 3 cm e altura 7 cm. Qual é o seu volume?
* r= 3 cm
* h= 7 cm
I) Substituindo os valores dados na fórmula, determinamos que o volume do cilindro será:
V= π r²h
V= π • 3²• 7
V= π • 9 • 7
V= 63π cm³
Esfera:
Figura tridimensional formada por um conjunto de pontos que podem se encontrar a uma distância do seu centro menor ou igual a R.

Fonte:https://pt.wikipedia.org/wiki/Esfera
O volume da esfera é dado pela seguinte fórmula:
V= 4π • R³
3
Exemplo: Calcule o volume de uma esfera com raio igual a 10 cm
V= 4π • R³
3
V= 4 • π • 10³
3
V = 4 • π • 1000
3
V= 4000π cm³
3
Cone:
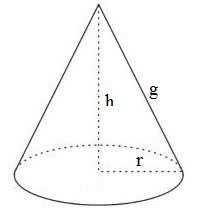
Como dito em aulas anteriores, o cone é uma figura geométrica que apresenta uma base circular constituída por segmentos de reta que apresentam como extremidade um vértice comum.
A altura do cone é a distância do plano da base até o vértice do cone. Esta figura possui a geratriz, ou seja, qualquer segmento formado por uma extremidade no vértice e outra na base da figura.
Sua área é dada por:
V= π r² • h
3
Exemplo: Calcule o volume de um cone circular cujo raio da base mede 3 m e a geratriz mede 5 m.
I) Primeiramente, precisamos determinar a geratriz deste cone através do teorema de Pitágoras.
h² + r²= g²
h² + 3²= 5²
h² + 9= 25
h²= 25 - 9
h²= 16
h= √16
h= 4 m
II) Agora, podemos determinar o volume do cone substituindo os valores da altura e do raio na fórmula.
V= π r²h
3
V= π • 3² • 4
3
V= π • 9 • 4
3
V= 36π
3
V= 12π cm³
Dominando o conhecimento- exercícios:
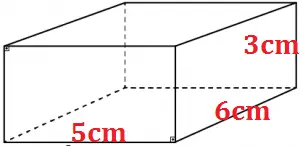
Questão 1) Calcule o volume do paralelepípedo abaixo:
Questão 2) Em um cone reto, a geratriz (g) mede 20 cm e a altura mede 16 cm. Determine seu volume.
Questão 3) (Sejus - Vunesp 2013) A quantidade de certo líquido correspondente a 3/4 de um litro será colocado em um recipiente de modo que ele fique completamente cheio. Para isso foram selecionados 3 recipientes com formas geométricas e medidas internas descritas a seguir:
I. Um paralelepípedo retângulo de dimensões: comprimento 15 cm, largura 2,5 cm e altura 20 cm.
II.Um cilindro reto de raio de base 5 cm e altura 10 cm. (Use π=3)
III. Um cubo de aresta igual a 5 cm
Dos 3 recipientes, atende ao que foi proposto
a) I e II apenas
b) I, II e III
c) I, apenas
d) I e III, apenas
e) II e III, apenas
Questão 4) Um reservatório em forma de cone possui volume de aproximadamente 3000 m^3 e um diâmetro de base medindo 24 cm. Determine a altura deste reservatório.
Use π= 3,14
Questão 5) (PM ES- 2013) Determinado cubo possui volume de 729 cm³. Cada face desse cubo possui área de:
a) 3 cm^2
b) 9 cm^2
c) 27 cm^2
d) 54 cm^2
e) 81 cm^2
Questão 6) Calcule o volume de uma esfera com 3 cm. Use π=3,14.
Questão 7) (Bombeiros ES- Cespe 2011)- Uma caixa d'água tem formato de um paralelepípedo retângulo, e outra, de um cilindro circular. A caixa d'água com formato de paralelepípedo tem base igual 20 m e 15 m, e altura igual a 5 m. O raio da caixa com formato cilíndrico mede 10 m, e a altura, 5 m. Tomando 3,14 como o valor aproximado da constante π, julgue os itens a e b.
a) A caixa com formato de paralelepípedo retângulo tem um mais capacidade de água que a caixa com formato cilíndrico
b) A caixa com formato cilíndrico tem capacidade de 1570 m³
Resoluções:
Questão 1)
I) Como conhecemos as medidas do paralelepípedo em questão, determinamos o seu volume substituindo estes valores na fórmula.
V=abc
V= 5 • 3 • 6
V= 90 cm³
Questão 2)
I) Primeiramente, precisamos determinar o raio deste cone através do teorema de Pitágoras:
h² + r²= g²
16² + r²= 20²
256 + r²= 400
r²= 400 - 256
r²= 144
r= √144
r= 12 cm
II) Agora, podemos determinar o volume do cone substituindo os valores da altura e do raio na fórmula.
V= π r²h
3
V= 3,14 • 12² • 16
3
V= 3,14 • 144 • 16
3
V= 7234, 56
3
V= 2411, 52 cm³
Questão 3)
* Sabendo que o 3/4 de um litro é igual a 750 cm^3, devemos verificar quais sólidos possuem medidas iguais a esta, atendendo ao que foi proposto:
I) Paralelepípedo
V=abc
V= 15 • 2,5 • 20
V= 15 • 50
V= 750 cm³ ( atende ao que foi proposto)
II) Cilindro
V= π r²h
V= 3• 5² • 10
V= 3 • 25 • 10
V= 3 • 250
V= 750 cm³ ( atende ao que foi proposto)
III) Cubo
V=a³
V=5³
V= 125 cm³ (não atende ao que foi proposto)
Resposta: Item a
Questão 4)
I) Sabendo que o volume do reservatório é V=3000 m^3 e que ele possui um diâmetro d= 24 cm, a altura será dada por:
r=d/2
r= 24/2
r= 12 cm
π r²h= V
3
3,14 • 12² • h= 3000
3
3,14 • 144 • h= 3000 • 3
452,16h= 9000
h= 9000
452,16
h=19,9 m
h~20 m
Resposta: A medida da altura do reservatório é aproximadamente 20 m.
Questão 5)
I) Como o volume do cubo é conhecido, a sua aresta será dada por:
V=a³
a³= 729
a=3√729
a= 9 m
II) A área de cada face deste cubo será:
A=a²
A= 9²
A= 81 cm²
Resposta:Item b.
Questão 6)
I) Tomando π como 3,14 e sabendo que o raio desta esfera mede 3 cm, o seu volume será
V= 4π • R³
3
V= 4 • 3,14 • 3³
3
V = 4 • 3,14 • 27
3
V= 339,12
3
V= 113,04 cm³
Resposta: V= 113,04 cm³.
Questão 7)
I) Primeiramente devemos determinar o volume da caixa em formato de paralelepípedo e a de formato cilíndrico.
* Volume da caixa com formato de paralelepípedo
Vp= 20 • 15 • 5
Vp= 1500 m³
*Volume da caixa com formato cilíndrico.
Vc= π r²h
Vc= 3,14 • 10² • 5
Vc= 3,14 • 100 • 5
Vc= 314 • 5
Vc= 1570 m³
II) Agora que determinamos o volume de ambas as caixas, jugaremos os itens a e b.
a) A caixa com formato de paralelepípedo tem mais capacidade de armazenamento que a caixa com formato cilíndrico.
Vc= 1570 m³ (caixa cilíndrica)
Vp= 1500 m³ ( caixa com formato de paralelepípedo)
*Vc> Vp
Resposta: Este item está incorreto.
b) A caixa com formato cilíndrico tem capacidade de 1570 m^3.
* Calculando o volume da caixa cilíndrica novamente:
Vc= π r^2 • h
Vc= 3,14 • 10^2 • 5
Vc= 3,14 • 100 • 5
Vc= 314 • 5
Vc= 1570 m³
Resposta: Verificamos que este item está correto.
O volume destes objetos é obtida através, essencialmente, de fórmulas específicas para cada sólido.
Apresentaremos algumas fórmulas para o cálculo da volume de alguns sólidos geométricos e como aplicá-las.
Cubo:
É um sólido geométrico que possui arestas e faces congruentes. Ou seja, ele possui medidas iguais de altura, largura e comprimento. Ele é constituído por 8 vértices e 12 arestas
A fórmula para calcular seu volume é dada por:
Exemplo I) Qual o volume de um cubo cuja medida da aresta é igual a 4 cm?
I) Como conhecemos a medida do cubo, basta substituí-la na fórmula
V= a³
V= 4³
V= 64 cm³
Paralelepípedo:
Figura tridimensional constituída de 12 arestas e 8 vértices que é definida como um prisma cuja as faces são paralelogramos. O seu volume é dado por:
Paraleleppedo com arestas cujas medidas são a,b e c.
V=abc
Exemplo: Calcule o volume de um paralelepípedo que apresenta medidas iguais a 10 cm, 7 cm e 3 cm.
I) Como conhecemos as medidas do paralelepípedo em questão, determinamos o seu volume substituindo estes valores na fórmula.
V= 10 • 7 • 3
V= 210 cm³
V= 210 cm³
Cilindro:
Raio: Distância entre o centro e uma extremidade do cilindro. (r)
Base: O cilindro apresenta uma base superior e inferior. Ambas são circulares, paralelas entre si e congruentes.
Geratriz: Segmento que passa de uma base para a outra. Corresponde a altura do cilindro.(altura h=g)
Diretriz: Corresponde aos pontos da geratriz nas extremidades do cilindro.
Exemplo: Dado um cilindro de raio 3 cm e altura 7 cm. Qual é o seu volume?
I) Substituindo os valores dados na fórmula, determinamos que o volume do cilindro será:
O volume da esfera é dado pela seguinte fórmula:
V= 4 • π • 10³
V = 4 • π • 1000
Exemplo: Calcule o volume de um cone circular cujo raio da base mede 3 m e a geratriz mede 5 m.
II) Agora, podemos determinar o volume do cone substituindo os valores da altura e do raio na fórmula.
V= π r²h
Questão 2) Em um cone reto, a geratriz (g) mede 20 cm e a altura mede 16 cm. Determine seu volume.
Questão 7) (Bombeiros ES- Cespe 2011)- Uma caixa d'água tem formato de um paralelepípedo retângulo, e outra, de um cilindro circular. A caixa d'água com formato de paralelepípedo tem base igual 20 m e 15 m, e altura igual a 5 m. O raio da caixa com formato cilíndrico mede 10 m, e a altura, 5 m. Tomando 3,14 como o valor aproximado da constante π, julgue os itens a e b.
a) A caixa com formato de paralelepípedo retângulo tem um mais capacidade de água que a caixa com formato cilíndrico
b) A caixa com formato cilíndrico tem capacidade de 1570 m³
V = 4 • 3,14 • 27
O seu volume é dado pela seguinte fórmula:
V= π r²h
Exemplo: Dado um cilindro de raio 3 cm e altura 7 cm. Qual é o seu volume?
* r= 3 cm
* h= 7 cm
I) Substituindo os valores dados na fórmula, determinamos que o volume do cilindro será:
V= π r²h
V= π • 3²• 7
V= π • 9 • 7
V= 63π cm³
Esfera:
Figura tridimensional formada por um conjunto de pontos que podem se encontrar a uma distância do seu centro menor ou igual a R.

Fonte:https://pt.wikipedia.org/wiki/Esfera

Fonte:https://pt.wikipedia.org/wiki/Esfera
O volume da esfera é dado pela seguinte fórmula:
V= 4π • R³
3
Exemplo: Calcule o volume de uma esfera com raio igual a 10 cm
V= 4π • R³
3
V= 4 • π • 10³
3
V = 4 • π • 1000
3
V= 4000π cm³
3
Cone:
Como dito em aulas anteriores, o cone é uma figura geométrica que apresenta uma base circular constituída por segmentos de reta que apresentam como extremidade um vértice comum.
A altura do cone é a distância do plano da base até o vértice do cone. Esta figura possui a geratriz, ou seja, qualquer segmento formado por uma extremidade no vértice e outra na base da figura.
Sua área é dada por:
V= π r² • h
3
Exemplo: Calcule o volume de um cone circular cujo raio da base mede 3 m e a geratriz mede 5 m.
I) Primeiramente, precisamos determinar a geratriz deste cone através do teorema de Pitágoras.
h² + r²= g²
h² + 3²= 5²
h² + 9= 25
h²= 25 - 9
h²= 16
h= √16
h= 4 m
II) Agora, podemos determinar o volume do cone substituindo os valores da altura e do raio na fórmula.
V= π r²h
3
V= π • 3² • 4
3
V= π • 9 • 4
3
V= 36π
3
V= 12π cm³
Dominando o conhecimento- exercícios:
Questão 1) Calcule o volume do paralelepípedo abaixo:
Questão 2) Em um cone reto, a geratriz (g) mede 20 cm e a altura mede 16 cm. Determine seu volume.
Questão 3) (Sejus - Vunesp 2013) A quantidade de certo líquido correspondente a 3/4 de um litro será colocado em um recipiente de modo que ele fique completamente cheio. Para isso foram selecionados 3 recipientes com formas geométricas e medidas internas descritas a seguir:
I. Um paralelepípedo retângulo de dimensões: comprimento 15 cm, largura 2,5 cm e altura 20 cm.
II.Um cilindro reto de raio de base 5 cm e altura 10 cm. (Use π=3)
III. Um cubo de aresta igual a 5 cm
Dos 3 recipientes, atende ao que foi proposto
a) I e II apenas
b) I, II e III
c) I, apenas
d) I e III, apenas
e) II e III, apenas
Questão 4) Um reservatório em forma de cone possui volume de aproximadamente 3000 m^3 e um diâmetro de base medindo 24 cm. Determine a altura deste reservatório.
Use π= 3,14
Use π= 3,14
Questão 5) (PM ES- 2013) Determinado cubo possui volume de 729 cm³. Cada face desse cubo possui área de:
a) 3 cm^2
b) 9 cm^2
c) 27 cm^2
d) 54 cm^2
e) 81 cm^2
Questão 6) Calcule o volume de uma esfera com 3 cm. Use π=3,14.
a) A caixa com formato de paralelepípedo retângulo tem um mais capacidade de água que a caixa com formato cilíndrico
b) A caixa com formato cilíndrico tem capacidade de 1570 m³
Resoluções:
Questão 1)
I) Como conhecemos as medidas do paralelepípedo em questão, determinamos o seu volume substituindo estes valores na fórmula.
V=abc
V= 5 • 3 • 6
V= 90 cm³
V= 90 cm³
Questão 2)
I) Primeiramente, precisamos determinar o raio deste cone através do teorema de Pitágoras:
h² + r²= g²
16² + r²= 20²
256 + r²= 400
r²= 400 - 256
r²= 144
r= √144
r= 12 cm
II) Agora, podemos determinar o volume do cone substituindo os valores da altura e do raio na fórmula.
V= π r²h
3
V= 3,14 • 12² • 16
3
V= 3,14 • 144 • 16
3
V= 7234, 56
3
V= 2411, 52 cm³
Questão 3)
* Sabendo que o 3/4 de um litro é igual a 750 cm^3, devemos verificar quais sólidos possuem medidas iguais a esta, atendendo ao que foi proposto:
I) Paralelepípedo
V=abc
V= 15 • 2,5 • 20
V= 15 • 50
V= 750 cm³ ( atende ao que foi proposto)
II) Cilindro
V= π r²h
V= 3• 5² • 10
V= 3 • 25 • 10
V= 3 • 250
V= 750 cm³ ( atende ao que foi proposto)
III) Cubo
V=a³
V=5³
V= 125 cm³ (não atende ao que foi proposto)
Resposta: Item a
Questão 4)
I) Sabendo que o volume do reservatório é V=3000 m^3 e que ele possui um diâmetro d= 24 cm, a altura será dada por:
r=d/2
r= 24/2
r= 12 cm
π r²h= V
3
3,14 • 12² • h= 3000
3
3,14 • 144 • h= 3000 • 3
452,16h= 9000
h= 9000
452,16
h=19,9 m
h~20 m
Resposta: A medida da altura do reservatório é aproximadamente 20 m.
Questão 5)
I) Como o volume do cubo é conhecido, a sua aresta será dada por:
V=a³
a³= 729
a=3√729
a= 9 m
II) A área de cada face deste cubo será:
A=a²
A= 9²
A= 81 cm²
Resposta:Item b.
Questão 6)
I) Tomando π como 3,14 e sabendo que o raio desta esfera mede 3 cm, o seu volume será
V= 4π • R³
3
V= 4 • 3,14 • 3³
V= 4 • 3,14 • 3³
3
V = 4 • 3,14 • 27
3
V= 339,12
3
V= 113,04 cm³
Resposta: V= 113,04 cm³.
3
V= 113,04 cm³
Resposta: V= 113,04 cm³.
Questão 7)
I) Primeiramente devemos determinar o volume da caixa em formato de paralelepípedo e a de formato cilíndrico.
* Volume da caixa com formato de paralelepípedo
Vp= 20 • 15 • 5
Vp= 1500 m³
*Volume da caixa com formato cilíndrico.
Vc= π r²h
Vc= 3,14 • 10² • 5
Vc= 3,14 • 100 • 5
Vc= 314 • 5
Vc= 1570 m³
II) Agora que determinamos o volume de ambas as caixas, jugaremos os itens a e b.
a) A caixa com formato de paralelepípedo tem mais capacidade de armazenamento que a caixa com formato cilíndrico.
Vc= 1570 m³ (caixa cilíndrica)
Vp= 1500 m³ ( caixa com formato de paralelepípedo)
*Vc> Vp
Resposta: Este item está incorreto.
b) A caixa com formato cilíndrico tem capacidade de 1570 m^3.
* Calculando o volume da caixa cilíndrica novamente:
Vc= π r^2 • h
Vc= 3,14 • 10^2 • 5
Vc= 3,14 • 100 • 5
Vc= 314 • 5
Vc= 1570 m³
Resposta: Verificamos que este item está correto.
* Volume da caixa com formato de paralelepípedo
Vp= 20 • 15 • 5
Vp= 1500 m³
*Volume da caixa com formato cilíndrico.
Vc= π r²h
Vc= 3,14 • 10² • 5
Vc= 3,14 • 100 • 5
Vc= 314 • 5
Vc= 1570 m³
II) Agora que determinamos o volume de ambas as caixas, jugaremos os itens a e b.
a) A caixa com formato de paralelepípedo tem mais capacidade de armazenamento que a caixa com formato cilíndrico.
Vc= 1570 m³ (caixa cilíndrica)
Vp= 1500 m³ ( caixa com formato de paralelepípedo)
*Vc> Vp
Resposta: Este item está incorreto.
b) A caixa com formato cilíndrico tem capacidade de 1570 m^3.
* Calculando o volume da caixa cilíndrica novamente:
Vc= π r^2 • h
Vc= 3,14 • 10^2 • 5
Vc= 3,14 • 100 • 5
Vc= 314 • 5
Vc= 1570 m³
Resposta: Verificamos que este item está correto.
Agradecimentos:
Agradeço a todos que prestigiaram meu blog e espero que gostem das atuais e futuras postagens do blog. Me perdoem pela cor da letra, mas tive problemas com a produção do texto e não consegui resolver.
Quem tiver dúvidas, pode comentá-las. Espero ter ajudado.
Agradeço a todos que prestigiaram meu blog e espero que gostem das atuais e futuras postagens do blog. Me perdoem pela cor da letra, mas tive problemas com a produção do texto e não consegui resolver.
Quem tiver dúvidas, pode comentá-las. Espero ter ajudado.
Quem tiver dúvidas, pode comentá-las. Espero ter ajudado.
Referências:
Referências:
3-https://sabermatematica.com.br/volumes-exercicios-resolvidos.html
4-http://dinamicamatematica.blogspot.com/2011/05/exercicios-resolvidos-de-geometria.html
5-https://escolaeducacao.com.br/geometria-espacial/
6-https://www.somatematica.com.br/emedio/espacial/formulas.php
7-https://mundoeducacao.bol.uol.com.br/matematica/volume-cubo.htm
8-https://sabermatematica.com.br/volume-do-paralelepipedo-retangulo.html
9-https://www.todamateria.com.br/volume-da-esfera/
10-http://questoesdevestibularnanet.blogspot.com/2013/11/questoes-resolvidas-de-vestibular-sobre.html
11-https://www.todamateria.com.br/volume-do-cone/
12-https://sabermatematica.com.br/exercicios-resolvidos-sobre-volume-do-cubo.html
13-https://www.todamateria.com.br/cilindro/
14-https://pt.wikipedia.org/wiki/Esfera
4-http://dinamicamatematica.blogspot.com/2011/05/exercicios-resolvidos-de-geometria.html
5-https://escolaeducacao.com.br/geometria-espacial/
6-https://www.somatematica.com.br/emedio/espacial/formulas.php
7-https://mundoeducacao.bol.uol.com.br/matematica/volume-cubo.htm
8-https://sabermatematica.com.br/volume-do-paralelepipedo-retangulo.html
9-https://www.todamateria.com.br/volume-da-esfera/
10-http://questoesdevestibularnanet.blogspot.com/2013/11/questoes-resolvidas-de-vestibular-sobre.html
11-https://www.todamateria.com.br/volume-do-cone/
12-https://sabermatematica.com.br/exercicios-resolvidos-sobre-volume-do-cubo.html
13-https://www.todamateria.com.br/cilindro/
14-https://pt.wikipedia.org/wiki/Esfera
.jpg)
Nenhum comentário:
Postar um comentário