Relações métricas no triângulo qualquer

Introdução:

A maioria dos problemas de trigonometria são resolvidos através da comparação com o triângulo retângulo, visto que algumas propriedades trigonométricas são válidas apenas para este tipo de triângulo. Mas não existe tanta facilidade na vida real, pois muitos problemas do cotidiano envolvem triângulos acutângulos ou obtusângulos.

Nestas situações, é necessário utilizar a lei dos senos e a dos cossenos.
Ambas as leis são válidas para quaisquer tipos de triângulos e são muito importantes para a física, engenharia e trigonometria.

     

Fonte:https://alunosonline.uol.com.br/matematica/tipos-de-triangulos.html

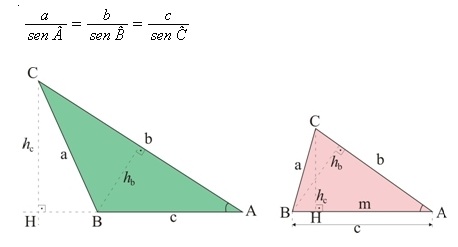
Lei dos senos:

Essa lei determina que existe uma proporcionalidade entre o seno de um ângulo e o lado oposto a esse ângulo.
Como dito antes, ela é válida para qualquer tipo de triângulo.

A lei dos senos demonstra que, em qualquer triângulo, existe uma razão constante entre um lado e o seno do seu ângulo oposto.
Ela é adequada para problemas nos quais conhecemos dois ângulos de um triângulo e um dos seus lados e queremos determinar a medida de um outro lado.

                                                                                                                                                       
                                                                 

Fonte:https://blogdoenem.com.br/relacoes-metricas/

Lei dos cossenos:

Essa lei é utilizada para encontrar a medida de um lado ou ângulo desconhecido de um triângulo qualquer, através de medidas conhecidas do mesmo.
Ela é válida para qualquer tipo de triângulo.

Essa lei tem o seguinte enunciado: "Em qualquer triângulo, o quadrado de um dos lados é igual a soma dos quadrados dos outros dois lados menos o dobro do produto desses dois lados pelo cosseno do ângulo entre eles."
Esta lei é adequada para problemas nos quais se conhece a medida de dois lados de um triângulo e o ângulo entre eles e queremos descobrir a medida do terceiro lado.
Ela também é adequada para a resolução de problemas nos quais conhecemos a medidas dos três lados de um triângulo e queremos conhecer um dos seus ângulos.

                      

Fonte:http://www.dinamatica.com.br/2011/03/uma-deducao-grafica-da-lei-dos-cossenos.html

E no triângulo retângulo?

Quando aplicamos a lei dos cossenos ao lado oposto ao ângulo reto, temos a seguinte equação:

   a²= b² + c² - 2 • b • c •  cos 90°

Como cos 90°=0,  a expressão acima fica como:

   
        a²= b² + c²

Podemos concluir que o teorema de Pitágoras é apenas um caso particular da lei dos cossenos.

Dominando o conhecimento - Exercícios:

Questão 1) (UF-Juiz de Fora) Dois lados de um triângulo medem 8 m e 10 m e formam um ângulo de 60°. Calcule a medida do terceiro lado.

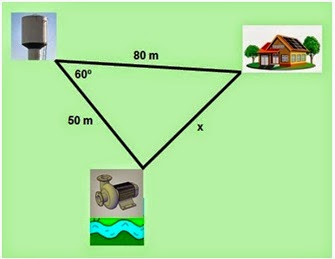
Questão 2)(UNICAMP) A água utilizada na casa de um sítio é captada e bombeada do rio para uma caixa d'água a 50 m de distância. A casa está a 80 m da caixa d'água e o ângulo formado pelas direções caixa d'água- bomba e caixa d' água-casa é de 60°. Se pretende bombear água do mesmo ponto de captação até a casa, quantos metros de encanamento serão necessários?

          

Fonte:http://professoraveleda.blogspot.com/p/lei-dos-senos-e-lei-dos-cossenos.html

Questão 3) Calcule o valor do segmento AB do triângulo representado pelo desenho a seguir:

      

Fonte: https://exercicios.brasilescola.uol.com.br/exercicios-matematica/exercicios-sobre-trigonometria-um-triangulo-qualquer.htm

*√3=1,732
*√2=1,414

Questão 4) ( Unifor-CE) Sabe-se que em todo triângulo a medida de cada lado é diretamente proporcional ao seno do ângulo oposto ao lado. Usando essa informação, determine a medida do lado AB do triângulo representado
Dado:
Sen 45°= √2 
                  2

Sen 120°= √3 
                    2
               

Fonte: https://exercicios.brasilescola.uol.com.br/exercicios-matematica/exercicios-sobre-trigonometria-um-triangulo-qualquer.htm

Questão 5) Dois lados de um triângulo medem 10 cm e 6 cm e formam entre si um ângulo de 120°. Calcule a medida do terceiro lado.

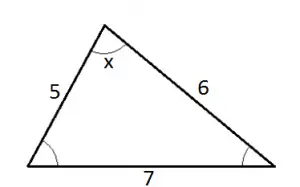
Questão 6) Calcular o cosseno do ângulo x, representado no triângulo abaixo:

                            

Fonte:https://sabermatematica.com.br/lei-dos-cossenos.html




Questão 7)  Determine o valor de x no triângulo a seguir:                                                                            

 

          

                                  

 

Resoluções:

Questão 1) Com as medidas que o problema fornece, basta aplicarmos a lei dos cossenos para obtermos a medida do terceiro lado deste triângulo:

*Lei dos cossenos

x²= 8² + 10² - 2 • 8 • 10 • cos 60°

x²= 64 + 100 - 2 • 80 • 0,5

x²= 164 - 160 • 0,5                            

x²= 164 - 80

x²= 84
x= √84

x= 2√21 m

Resposta: O terceiro lado deste triângulo mede 2√21 metros.

Questão 2) Com as medidas que o problema fornece, basta aplicarmos a lei dos cossenos para obtermos quantos metros de encanamento são necessários:

x²=80² + 50² - 2 • 80 • 50 • cos 60°

x²= 2500 + 6400 - 2 • 80 • 50 • 0,5

                                                   

x²=2500 + 6400 - 8000 • 0,5

                                          

x²= 2500 + 6400 - 4000

x²=2500 + 2400

x²= 4900

x= √4900

x=70 metros

Resposta: Serão necessários 70 metros de encanamento para bombear a água do ponto de captação até a casa.

Questão 3)

I) Para resolvermos o problema, basta aplicarmos a lei dos senos:

               100    =     med (AB)      

             sen 45°          sen 120°

             100   = med  (AB)

              √2            √3  

                 2              2

          √3 • 100= √2 • med (AB)

           2                2

Multiplicando os dois lados da equação por dois, temos que:

           

   2 • √3 • 100 =   √2    • med (AB) • 2     

         2                 2  

100 √3= med (AB)√2

med (AB)= 100 √3 

                       √2

med (AB)= 100 √3 • √2  

                          √2 • √2

med (AB)= 100√6 

                        2

med (AB)=50√6 m

Resposta: O segmento AB mede 50√6 metros.

Questão 4)

I) Para resolvermos o problema, basta aplicarmos a lei dos senos utilizando as informações que o problema forneceu:

               12      =  med (AB) 

           sen 120 °        sen 45°

              12  = med (AB)

              √3          √2 

                2            2

    med (AB) √3  =12 •   √2  

                      2                 2

  II) Multiplicando os dois lados da equação por dois, temos:

2 • med (AB)  √3   = 12 •  √2   • 2

                          2                  2

med (AB) √3= 12 √2

med (AB)= 12√2               

                      √3

med (AB)= 12√2 • √3 

                      √3 • √3

med (AB)= 12√6 

                       3

med (AB)= 4√6 metros

Resposta: O lado AB deste triângulo mede 4√6 metros.

Questão 5) Com as medidas que o problema fornece, basta aplicarmos a lei dos cossenos para obtermos a medida do terceiro lado deste triângulo:

x²=10² + 6² - 2 • 80 • 50 • cos 120°

x²= 100 + 36 - 2 • 10 •6 • (-0,5)

                                                   

x²=100 + 36 - 120 • (-0,5)

                                          

x²= 100 + 36 + 60

x²=136 + 60

x²= 196

x= √196

x=14 metros

Resposta: O terceiro lado deste triângulo mede 14 metros.

Questão 6)

I)Com as medidas que o problema fornece, basta aplicarmos a lei dos cossenos para obtermos a medida do ângulo x:

7²= 5² + 6² - 2 • 5 • 6 • cos x

49=25 + 36 - 10 • 6 • cos x

49=61 - 60 • cos x

60 • cos x= 61 - 49

60 • cos x= 12

cos x= 12 

            60

cos x=0,2

Resposta: O cosseno do ângulo x é igual a 0,2.

Questão 7)
I) Primeiramente, iremos aplicar a lei dos Cossenos para relacionar os lados do triângulo em questão.
          7²= 3² + x² - 2 • 3 • x • cos 60°           
           49=  9 + x²  - 2 • 3 • x • 0,5 
           49= 9 + x² - 3x
            x² - 3x + 9= 49
            x² - 3x - 49 + 9= 0
             x² - 3x - 40 =  0
II) Agora, aplicaremos a fórmula de Bhaskara para determinar o valor de x        


∆=b² - 4ac
∆=(-3)² - 4 • 1 • (-40)
∆= 9 + 160                                                   
∆= 169     

x= - b ± √∆                    
         2a    

x=  3 ± √169              
         2 • 1         

x=  3 ± 13   
          2     

x'= 3 + 13  =  16 
         2            2

x '= 8

x"= 3 - 13  = -  10       
          2              2

x"=  -5 (não convém)
 
Resposta: Por se tratar de medidas,  descartamos x"= - 5  e utilizamos x'= 8. O valor de x no triângulo é 8 cm.                                                                                                                                                                                                                                                                                                                                                                                                                                                 

Agradecimentos:

Agradeço a todos que prestigiaram meu blog e espero que gostem das atuais e futuras postagens do blog. Quem tiver dúvidas, pode comentá-las. Espero ter ajudado.

Referências:

1-https://mundoeducacao.bol.uol.com.br/matematica/lei-dos-cossenos.htm
2-https://www.todamateria.com.br/lei-dos-cossenos/
3-https://sabermatematica.com.br/lei-dos-cossenos.html
4-http://meteorotica.blogspot.com/2012/01/exercicios-resolvidos-sobre-lei-dos.html
5-https://mundoeducacao.bol.uol.com.br/matematica/a-lei-dos-senoscompreendendo-sua-aplicacao.htm
6-https://mundoeducacao.bol.uol.com.br/matematica/trigonometria-no-triangulo-qualquer.htm
7-https://exercicios.brasilescola.uol.com.br/exercicios-matematica/exercicios-sobre-trigonometria-um-triangulo-qualquer.htm
8-http://www.dinamatica.com.br/2011/03/uma-deducao-grafica-da-lei-dos-cossenos.html
9-https://www.mistersabido.com/lei-dos-senos/
10-http://hugeexerciselist.com/index.php?ui=lei%20dos%20cossenos
11-https://blogdoenem.com.br/relacoes-metricas/