O que é?
É uma forma de escrever números absurdamente grandes ou pequenos em potências de 10. Ela é frequentemente usada em textos científicos para facilitar comparações entre dados e operações matemáticas.
A forma da notação científica sempre é dada por:
Onde:
N= número real igual ou maior que 1 e menor que 10 (mantissa)
n=número inteiro que indica a ordem de grandeza do número.

Como escrever um número em notação:
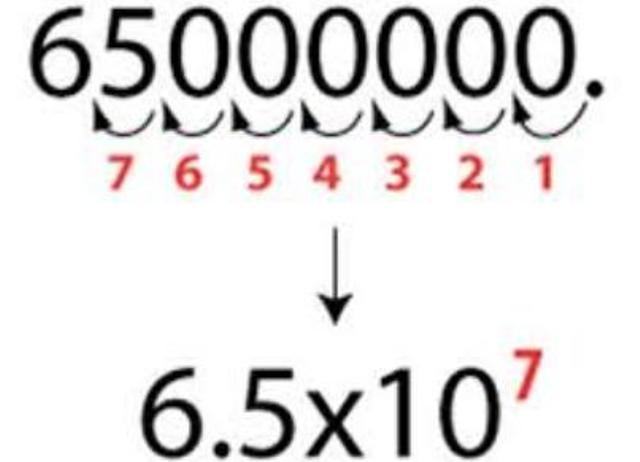
Para números grandes, deve-se deslocar a vírgula para esquerda até o primeiro algarismo. A imagem abaixo demonstra como se faz.
Exemplos:
I) 32 000=3,2 • 10^4
II)3 400 000=3,4 • 10^6
Para números menores, deve-se deslocar a vírgula para a direita até o primeiro algarismo.
Exemplos:
I) 0,0095=9,5 • 10^-3 (desloca-se três casas para a direita)
II)0,00034=3,4 •10^-4 (desloca-se quatro casas para a direta)
Observação: É importante lembrar que quando deslocamos a vírgula para a esquerda, deve-se somar da potência de 10 o número de casas deslocadas.
1 200 • 10^5 =1,2 • 10^(5+3)=1,2 • 10^8 (deslocando-se a vírgula para esquerda
Quando vírgula se deslocar para a esquerda, deve-se subtrair da potência de 10 o número de casas deslocadas
0,078 • 10^5=7,8 • 10^(5-2)=7,8 • 10^3 (deslocando-se a vírgula para a direita)
Divisão: A divisão de números escritos em notação científica consiste na divisão dos números reais da mantissa, repetir a base 10 e subtrair seus expoentes.
Exemplos:
I) (9,3 • 10^-6)= (9,3) • 10^-6-(-3)=3 •10^-6+3=3 • 10^-3
Soma e subtração: Para efetuar estas operações, é necessário transformar os números de modo que fiquem a mesma potência de 10. Depois, basta somar ou subtrair os números e conservar a base 10 com o mesmo expoente.
Exemplos:
I) (7,125 • 10^-3) + (4,512 • 10^-2)=(0,7125 • 10^-2) + (4,512 • 10^-2)=5,2245 • 10^-2
II)(3,3 • 10^8) + (4,8 • 10^8)=7,1 • 10^8
III) (6,4 • 10^8) - (8,3 • 10^8)=-1,9 • 10^8
Potenciação: Para elevarmos um número em notação científica para um expoente m, basta elevar o número real da mantissa a m e multiplicar o expoente a ordem de grandeza por m
Exemplos:
I) (5,26 • 10^3)^2= (5,26^2) • 10^(3 •2)=27,6 • 10^6=2,76 • 10^7
II) (5 • 10^3)^2= (5^2) • 10^(3 •2)=25 • 10^6= 2,5 • 10^7
=90 006 506 • 10^-4= 9000,6506= 9,0006506 • 10^3
Item c) (3 • 10^3) + (4 • 10^1) + (5 • 10^-2)
* Transformando os números de modo que fiquem a mesma potência de 10, obtemos que a soma destas parcelas é igual a:
(3 • 10^3) + (4 • 10^1) + (5 • 10^-2)= (300 000 • 10^-2)+ (4 000 • 10^-2)+ (5 • 10^-2)=
= (304 005 • 10^-2)= 3 040,05= 3,04005 • 10^3
Questão 4)
a) (2,3 • 10^4) • (2 •10^2)=( 2 • 2,3) • 10^4+2=4,6 • 10^(4+2)=4,6 • 10^6
b) (4 • 10^-3) • (5 • 10^-4)= (4 • 5) • 10^-3+(-4)=20 • 10^-8=2 •10^7
Para números menores, deve-se deslocar a vírgula para a direita até o primeiro algarismo.
Exemplos:
I) 0,0095=9,5 • 10^-3 (desloca-se três casas para a direita)
II)0,00034=3,4 •10^-4 (desloca-se quatro casas para a direta)
Observação: É importante lembrar que quando deslocamos a vírgula para a esquerda, deve-se somar da potência de 10 o número de casas deslocadas.
1 200 • 10^5 =1,2 • 10^(5+3)=1,2 • 10^8 (deslocando-se a vírgula para esquerda
Quando vírgula se deslocar para a esquerda, deve-se subtrair da potência de 10 o número de casas deslocadas
0,078 • 10^5=7,8 • 10^(5-2)=7,8 • 10^3 (deslocando-se a vírgula para a direita)
Operações na notação científica:
Multiplicação: A multiplicação de números escritos em notação científica consiste em multiplicar os números reais da mantissa, repetir a base 10 e somar seus expoentes.
Exemplos:
I) (1,1 • 10^4) • (2,1 • 10^3)=(1,1 • 2,1) • 10^4+3= 2,31 • 10^7
II) (1,4 • 10^2) • ( 3 • 10^4)=(1,4 • 3) • 10^2+4= 4,2 •10^6
Exemplos:
I) (9,3 • 10^-6)= (9,3) • 10^-6-(-3)=3 •10^-6+3=3 • 10^-3
(3,1 • 10^-3) (3,1)
Soma e subtração: Para efetuar estas operações, é necessário transformar os números de modo que fiquem a mesma potência de 10. Depois, basta somar ou subtrair os números e conservar a base 10 com o mesmo expoente.
Exemplos:
I) (7,125 • 10^-3) + (4,512 • 10^-2)=(0,7125 • 10^-2) + (4,512 • 10^-2)=5,2245 • 10^-2
II)(3,3 • 10^8) + (4,8 • 10^8)=7,1 • 10^8
III) (6,4 • 10^8) - (8,3 • 10^8)=-1,9 • 10^8
Potenciação: Para elevarmos um número em notação científica para um expoente m, basta elevar o número real da mantissa a m e multiplicar o expoente a ordem de grandeza por m
Exemplos:
I) (5,26 • 10^3)^2= (5,26^2) • 10^(3 •2)=27,6 • 10^6=2,76 • 10^7
II) (5 • 10^3)^2= (5^2) • 10^(3 •2)=25 • 10^6= 2,5 • 10^7
Radiciação:
Para obter a raiz de um número em notação científica, basta converter o valor em uma forma na qual o expoente é divisível pela raiz. Na raiz quadrada, por exemplo, o expoente de 10 deve ser divisível por dois. Para realizar essa operação, deve-se determinar a raiz da mantissa e dividir o expoente da ordem de grandeza pelo índice da raiz.
I) 3√ (1,25 • 10^2)= 3√ (0,125 • 10^3)= 0,5 •10^(3/3)=0,5 • 10^1=5
II) √(3,6 • 10^7)= √ (36 • 10^6)= 6 • 10^(6/2)= 6 • 10^3
Dominando o conhecimento - Exercícios:
Questão 1) (FUVEST 2009)
As células da bactéria Escherichia coli têm formato cilíndrico, com 8 • 10^-7 metros. O diâmetro de um fio de cabelo é de aproximadamente 1 • 10^-4 metros.
Dividindo-se o diâmetro de um cabelo pelo diâmetro de uma célula de Escherichia coli, obtém-se:
a) 125
b)250
c)500
d)1000
e)8000
Questão 2) Escreva os seguintes números em notação científica.
a)8 547 403
b)802,58
c)17,043
d)109, 306
Questão 3) Calcule
a) (10^4) +(8 • 10^3) + (3 • 10^2) + (5 • 10^1) + 6
b) ( 6 • 10^-1) + (5 • 10^-2) + (9 • 10^3) + (6 • 10 ^-4)
c) (3 • 10^3) + (4 • 10^1) + (5 • 10^-2)
Questão 4) Determine:
a) (2,3 • 10^4) • (2 • 10^2)
b) (4 • 10^-3) • (5 • 10^-4)
Resoluções:
Questão 1) Dividindo-se o diâmetro do fio de cabelo pelo diâmetro de uma célula de Eschericha coli, através da notação científica obtém-se:
diâmetro do cabelo = ( 1 • 10^-4) = 1 • 10^-4 -(-7)=0,125 • 10^(7-4)=0,125 • 10^3=
diâmetro da célula (8 • 10^-7) 8
Questão 4) Determine:
a) (2,3 • 10^4) • (2 • 10^2)
b) (4 • 10^-3) • (5 • 10^-4)
Resoluções:
Questão 1) Dividindo-se o diâmetro do fio de cabelo pelo diâmetro de uma célula de Eschericha coli, através da notação científica obtém-se:
diâmetro do cabelo = ( 1 • 10^-4) = 1 • 10^-4 -(-7)=0,125 • 10^(7-4)=0,125 • 10^3=
diâmetro da célula (8 • 10^-7) 8
= 1,25 • 10^2= 125
Resposta: Item e.
Questão 2) Respostas
Item a) 8 547 403= 8, 547 403 • 10^6
Item b)802,58=8,0258 • 10^2
Item c)17,043= 1,7043 • 10^1
Item d)109, 306=1,09306 • 10^2
Questão 3) Para resolver esta questão precisamos nos basear no princípio da adição de números em notação científica, que consiste em transformar os números de modo que fiquem a mesma potência de 10. Os números serão transformados de modo que fiquem a menor potência de 10 para que os cálculos fiquem mais simples.
Item a) (10^4) + (8 • 10^3) + (3 •10^2) + (5 •10^1)+ 6
*Neste caso, converteremo os números para notação decimal e realizar a soma porque este procedimento é mais prático neste caso.
10 000 + 8 000 + 300 +50+ 6 = 18 356
Item b) ( 6 • 10^-1) + (5 • 10^-2) + (9 • 10^3) + (6 • 10 ^-4)
* Transformando os números de modo que fiquem a mesma potência de 10, obtemos que a soma destas parcelas é igual a:
(6000 • 10^-4) + (500 •10^-4) + (90 000 0000 • 10^-4) + (6 • 10^-4)=Resposta: Item e.
Questão 2) Respostas
Item a) 8 547 403= 8, 547 403 • 10^6
Item b)802,58=8,0258 • 10^2
Item c)17,043= 1,7043 • 10^1
Item d)109, 306=1,09306 • 10^2
Questão 3) Para resolver esta questão precisamos nos basear no princípio da adição de números em notação científica, que consiste em transformar os números de modo que fiquem a mesma potência de 10. Os números serão transformados de modo que fiquem a menor potência de 10 para que os cálculos fiquem mais simples.
Item a) (10^4) + (8 • 10^3) + (3 •10^2) + (5 •10^1)+ 6
*Neste caso, converteremo os números para notação decimal e realizar a soma porque este procedimento é mais prático neste caso.
10 000 + 8 000 + 300 +50+ 6 = 18 356
Item b) ( 6 • 10^-1) + (5 • 10^-2) + (9 • 10^3) + (6 • 10 ^-4)
* Transformando os números de modo que fiquem a mesma potência de 10, obtemos que a soma destas parcelas é igual a:
=90 006 506 • 10^-4= 9000,6506= 9,0006506 • 10^3
Item c) (3 • 10^3) + (4 • 10^1) + (5 • 10^-2)
* Transformando os números de modo que fiquem a mesma potência de 10, obtemos que a soma destas parcelas é igual a:
(3 • 10^3) + (4 • 10^1) + (5 • 10^-2)= (300 000 • 10^-2)+ (4 000 • 10^-2)+ (5 • 10^-2)=
= (304 005 • 10^-2)= 3 040,05= 3,04005 • 10^3
Questão 4)
a) (2,3 • 10^4) • (2 •10^2)=( 2 • 2,3) • 10^4+2=4,6 • 10^(4+2)=4,6 • 10^6
b) (4 • 10^-3) • (5 • 10^-4)= (4 • 5) • 10^-3+(-4)=20 • 10^-8=2 •10^7
Agradecimentos:
Agradeço a todos que prestigiaram meu blog e espero que gostem das atuais e futuras postagens do blog. Quem tiver dúvidas, pode comentá-las. Espero ter ajudado.
Referências:
1-https://www.coladaweb.com/matematica/notacao-cientifica
2-https://revisaofisica.wordpress.com/2015/05/21/multiplicacao-e-divisao-em-notacao-cientifica/
3-http://www.matematicadidatica.com.br/NotacaoCientifica.aspx
4-https://www.estudokids.com.br/como-mudar-de-posicao-a-virgula-na-notacao-cientifica/
5-https://www.infoescola.com/matematica/notacao-cientifica/
6-http://www.universiaenem.com.br/sistema/faces/pagina/publica/conteudo/texto-html.xhtml?redirect=36125428256796652224798763426
7-https://doutormatematico.blogspot.com/2013/04/exercicios-sobre-notacao-cientifica.html
8-http://projetoseeduc.cecierj.edu.br/eja/recurso-multimidia-professor/fisica/novaeja/m1u01/ListadeExercicios-Unidade6.pdf
9-http://www2.anhembi.br/html/ead01/fisica/lu01/lo2/index.htm
10-http://www2.anhembi.br/html/ead01/fisica/lu01/lo2/wo_exemplos1.htm
Nenhum comentário:
Postar um comentário