Tira-dúvidas:dilatação térmica

O que é?

É o fenômeno no qual as dimensões de um corpo variam quando ele sofre uma variação em sua temperatura. Quando os corpos sofrem aumento de temperatura, eles dilatam e no momento em que eles esfriam, se contraem.

Isso ocorre porque variar a temperatura do corpo significa alterar também a agitação térmica dos seus átomos e a distância entre eles, o que consequentemente aumenta ou diminui as dimensões deles.

Existem três tipos de dilatação que são:

Dilatação linear:

Define a dilatação sofrida por um corpo em apenas uma única dimensão e por isso, ela só é aplicada para corpos sólidos. Acontece, por exemplo, nos fios e trilhos de trem, onde o comprimento é mais relevante que a espessura e altura.

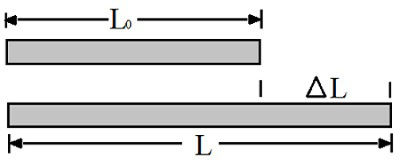
Resultado de imagem para dilatação térmica

Fonte:https://brasilescola.uol.com.br/o-que-e/fisica/o-que-e-dilatacao-termica-linear.htm

∆L= L0 • a • ∆T

Onde
∆L= Variação de comprimento (L- L0)
L0 =Comprimento inicial
a= coeficiente de dilatação
∆T=Variação de temperatura (T- T0)

Dilatação superficial:

É a dilatação que um corpo sofre em duas dimensões, sendo também aplicada somente para corpos sólidos. Este fenômeno ocorre por exemplo com chapa de metal e CD's.

Ela é dada pela fórmula:

∆A= A0 • b • ∆T

∆A=Variação da área (A-A0)
∆T=Variação de temperatura (T- T0)
b=coeficiente de dilatação superficial= 2a
A0= Área inicial

Resultado de imagem para dilatação superficial

Fonte:https://www.estudopratico.com.br/dilatacao-dos-solidos-linear-superficial-e-volumetrica/

Dilatação volumétrica:

É a dilatação que um corpo sofre em três dimensões, podendo ser aplicada para sólidos, líquidos e gases. Ocorre, por exemplo, com uma barra de ouro ou com um cubo de ferro.

Ela é dada pela seguinte fórmula:

∆V= V0 • y • ∆T

∆A=Variação da área (A-A0)
∆T=Variação de temperatura (T- T0)
y=coeficiente de dilatação volumétrica= 3a
V0= Volume inicial

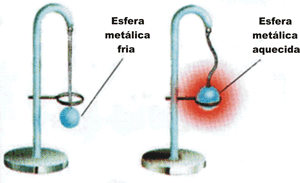
Fonte:http://mecanica-blog.blogspot.com/2010/04/dilatacao-termica.html

Dilatação dos sólidos:

Por terem formato definido, é possível calcular as dimensões de um sólido como o seu comprimento, largura e altura. Isso quer dizer que é necessário calcular a dilatação linear, superficial e volumétrica dos sólidos

Dilatação dos líquidos

Como os líquidos e gases não apresentam formato definido, adquirem somente a forma que seus recipientes contém, o que torna desnecessário medir a dilatação linear e superficial deles, precisando somente calcular a volumétrica.

Coeficiente de dilatação:

A dilatação de um corpo depende do material que o constitui. Por isso, os cálculos de dilatação sempre envolvem a substância que o corpo é feito, através do coeficiente de dilatação linear (a) dele.

A unidade da dilatação é o °C^-1, o inverso do grau Celsius.

Dominando o conhecimento - Exercícios:

Questão 1) Um fio de aço apresenta comprimento igual a 20 m quando sua temperatura é de 40 °C. Qual será o seu comprimento quando sua temperatura for igual a 100 °C? Considere o coeficiente de dilatação linear do aço igual a (11 • 10^-6) °C^-1?

Questão 2)Uma chapa quadrada de alumínio possui lados iguais a 3 m quando sua temperatura é igual a 80 °C. Qual será a variação de área, se a chapa for submetida a uma temperatura de 100 °C ?

Considere o coeficiente de dilatação superficial do alumínio igual a (22 • 10^-6) °C^-1.

Questão 3) Uma barra de ouro a 20 °C de temperatura tem as seguintes dimensões: 20 cm de comprimento, 10 cm e 5 cm de profundidade. Qual será a sua dilatação volumétrica após ser submetida a 50 °C? Considere o coeficiente de dilatação volumétrica do ouro igual a (15• 10^-6) °C^-1.

Resolução:

Questão 1)
Dados:

a=(11 • 10^-6) °C^-1=(1,1 • 10^-5) °C^-1

L0=20 m= 2 • 10^1 m

∆T=T- T0=100- 40=60 °C

T=100°C

T0=40°C

∆L= L0 • a • ∆T= (2 • 10^1) • (1,1 • 10^-5 ) • (6• 10^1 )

∆L= (2,2 • 10^-4) • (6• 10^1 )

∆L=13,2 • 10^-3=1,32 • 10^-2=0,0132 m

∆L=L-L0=
L-20=0,0132
L=0,0132 + 20
L=20,0132 m

Resposta: O comprimento da barra é igual a 20,0132 m quando está sob 100°C.

Questão 2)
Dados:

a=(22 • 10^-6) °C^-1= (2,2 • 10^-5) °C^-1

b=2a= 2 • (2,2 • 10^-5 °C^-1 )= (4,4• 10^-5) °C^-1

A0=3 • 3= 9 m^2

∆T=T- T0=100- 80=20 °C= (2 • 10^1) °C

T=100°C

T0=80°C

Pela fórmula da dilatação superficial, obtemos que

∆A= A0 • b • ∆T
∆A= 9 • (4,4• 10^-5  ) • ( 2 • 10^1 )
∆A= (39,6 • 10^-5 ) • ( 2 • 10^1 )
∆A=(79,2 • 10^-4)
∆A=7,92 • 10^-3=0,00792 m^2

Resposta: A variação de área é igual a 0,00792 m^2.

Questão 3)
Dados:
V0=20 • 10 • 5=1000 cm^3= (1 • 10^3) cm^3
T0=20 °C
T=50 °C
∆T=T- T0=50-20=30 °C= (3 • 10^1) °C
y=(15• 10^-6) °C^-1=(1,5• 10^-5) °C^-1

   ∆V= V0 • y • ∆T
∆V= (1 • 10^3) • (1,5 • 10^-5) •  (3 • 10^1)
   ∆V=(1,5 • 10^-2) • (3 • 10^1)
∆V=(4,5 • 10^-1)
  ∆V=0,45 cm^3
Resposta: A variação de volume é igual a 0,45 cm^3.

Agradecimentos:

Agradeço a todos que prestigiaram meu blog e espero que gostem das atuais e futuras postagens do blog. Quem tiver dúvidas, pode comentá-las. Espero ter ajudado.