terça-feira, 16 de outubro de 2018

Tira-Dúvidas:Quadriláteros

 O que são?

Quadriláteros são polígonos que possuem quatro lados e duas diagonais. Um fato muito importante no estudo destas figuras geométricas é o fato da soma de seus ângulos internos sempre ser igual 360°.
Os principais elementos do quadrilátero são:
*Lados: Segmentos que contornam a figura
*Vértices: São os pontos de encontro entre dois lados.
*Ângulos internos: Ângulos entre dois lados consecutivos de um polígono
*Ângulos externos: Prolongamento de um dos lados de um polígono. Este ângulo é suplementar ao ângulo interno.
*Diagonais: Segmento que une dois pontos não consecutivos e que não são lados.

Quadriláteros notáveis:

Estas figuras podem ser classificadas de três maneiras, sendo elas baseadas na posição relativa entre os lados das mesmas. As classificações são as seguintes:

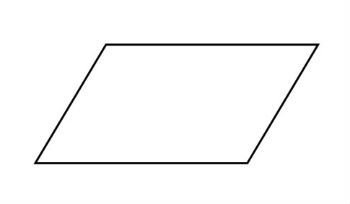
Paralelogramos:

São quadriláteros que possuem como principal propriedade o fato de os seus lados opostos serem paralelos. Outras características deles são:
* Os ângulos opostos são congruentes e não suplementares
* Os lados opostos são congruentes
* As diagonais do paralelogramo encontram-se no seu ponto médio.
* A soma de dois ângulos adjacentes é 180°
             Paralelogramo

Retângulo:

É um caso especial de paralelogramo no qual todos os seus lados são ângulos internos são retos e as suas diagonais são congruentes.Ele apresenta todas as propriedades dos paralelogramos e, por isso, pode-se dizer que todo retângulo é um paralelogramo.

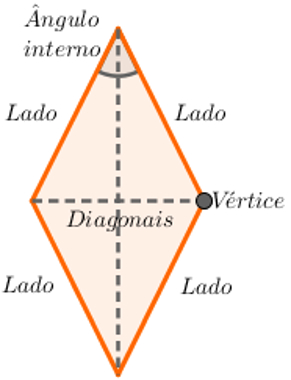
Losango: 

Um outro tipo de figura com todas as propriedades dos paralelogramos, mas ele também possui propriedades próprias dele como:
* As diagonais de um losango são perpendiculares
* As diagonais de um losango sempre coincidem com as bissetrizes de seus ângulos internos
* Todos os seus lados são congruentes
*A soma de dois ângulos internos adjacentes é 180°

                                     Imagem relacionada

Quadrado:

Possui os quatro lados iguais e todos os ângulos retos. Suas diagonais são perpendiculares e congruentes, o que permite classificar esta figura como retângulo e losango ao mesmo tempo.

                                Imagem relacionada

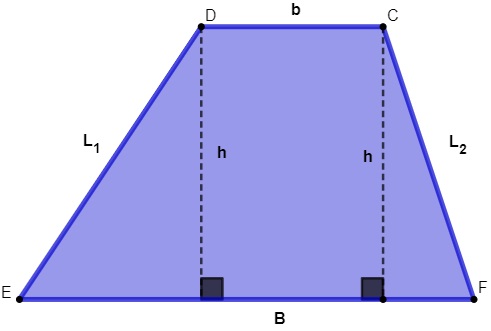
Trapézio:

Figura que apresenta os dois lados paralelos que são denominados bases, sendo uma maior e outra menor. Diferencia-se por apresentar subcategorias como: 
*Trapézio retângulo: Apresenta dois ângulos retos
*Trapézio isósceles: Seus lados não paralelos são congruentes. Ângulos adjacentes a mesma base são congruentes
* Trapézio escaleno: Os lados não paralelos não são congruentes.

O trapézio possui três segmentos que são cruciais para o seu estudo que são:
* Altura: Segmento que indica a menor distância entre a base dos trapézios
*Base média:Segmento que une os pontos médios dos lados não paralelos.
Ela é dada por:

   Bm=MN=B+b= AB+DC
                      2             2

DC=B=base maior
AB=b=base menor
MN=base média
Bm=base média

*Mediana de Euler:Segmento da base média que se encontra entre as diagonais do trapézio. É dada por:
         
             PQ=Me= B-b= DC-AB
                               2           2
DC=B=base maior
AB=b=base menor
PQ=mediana de Euler
Me=mediana de Euler
                          




Exercícios resolvidos:

Questão 1) A base média de um trapézio mede 11 cm, e a mediana de euler mede 3 cm. Calcule as medidas das bases do trapézio.

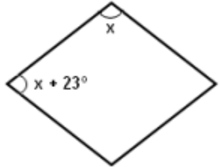
Questão 2)Observe o losango e determine a medida do ângulo x.

                          
questao resolvida losango

Questão 3) Determine V ou F para as afirmações:

a) Todo retângulo é um paralelogramo
b)Todo paralelogramo é um retângulo
c)Todo quadrado é um retângulo
d)Todo paralelogramo é um losango
e)Todo quadrado é um losango

Resoluções

Questão 1)Analisando o problema, pode-se perceber que ele forneceu o valor da base média e da mediana de Euler, o que nos permite montar um sistema de equações a partir das relações que estes dois segmentos tem para com as bases. 
B-base maior
b-base menor

 O sistema é escrito como:
{B+b=11
{  2
{
{B-b=3
{ 2

 Simplificando o sistema ao multiplicar as duas equações por 2 temos que:
{2(B+b)=2(11)
{       2
{
{2( B-b)= 2(3)
{     2

As equações ficam escritas como:

{B+b=22
{B-b=6

Agora que as equações estão simplificadas, podemos resolvê-las por método de adição
 {B+b=22
+
 {B-b=6
  2B=28
    B=14 cm
Determinado B, podemos determinar b.
b=22-B
b=22-14
b=8 cm

Resposta: A base maior mede 14 cm e a menor mede 8 cm.


Questão 2) Considerando que a soma de dois ângulos adjacentes de um losango é 180°. Podemos escreve que:

             x+x+23=180
             2x+23=180
             2x=180-23
             2x=157
               x=157/2
                x=78,5°
Resposta: O ângulo x mede 78,5 °

Questão 3) Gabarito
a)V
b)F
c)V
d)F
e)V

Agradecimentos:


Agradeço a todos que prestigiaram meu blog e espero que gostem das atuais e futuras postagens do blog. Essa postagem está fora do planejamento oficial do meu blog, porque está numa área de tira-dúvidas na qual tiro dúvidas de quais quer conteúdos de exatas. Quem não compreendeu algo da minha aula, comente.
Fiz esta postagem a pedido de alguns seguidores.

Referências:



Postado por às Nenhum comentário:

segunda-feira, 15 de outubro de 2018

Dominando o conhecimento- Exercícios corrigidos sobre conjuntos numéricos

Questão 1) Dado dois conjuntos C={15, 25,  30, 35} e D={ 15, 25, 40, 50}. Determine C∩D.

Questão 2)Dados os conjuntos A={ 0, 1}, B= {0, 1, 2}, C= {2, 3}. Determine (A U B) ∩ (B U C)

Questão 3)Sejam os conjuntos A={1, 2, 3} e B= {2, 3, 5], determine o conjunto A-B.

a){}

b){1, 5}

c){5}

d){1}

e){2, 3}

Questão 4)Considere o conjunto B={ 1, 2, 3, 4, 5}, A={1, 2}, C={3, 4, 5} e D= {0, 1, 2, 3, 4, 5}. Indique as afirmações que são verdadeiras (V) e as falsas (F).

a) 2 ∈ A

 b)3 ∈ B
c)0 ∈ C

 d)4 ∈ D

 e)5 ∈ A

 f)6 ∉ A

 g)7 ∈ A

 h)0 ∈ B

Questão 5) Dado os conjuntos A={0, 1, 2, 3, 4, 5}, B={4, 5, 6, 7} e C={4, 5, 6, 8}, Determine (A-C) ∩ (B-C)

Resoluções 

Questão 1) Analisando os conjuntos C={15, 25, 30, 35} e D={15, 25, 40, 50}, temos que o conjunto será a união dos elementos existentes em todos os conjuntos. Portanto, o conjunto união entre C e D, 
C U D= {15, 25, 30, 35, 40, 50}

 Resposta:C ∩ D={15, 25, 30, 35, 40, 50}

Questão 2) Analisando os conjuntos A={0, 1}, B=[0, 1, 2} e C={2, 3} e o que a questão exige primeiramente  iremos determinar os seguintes conjuntos:
A U B= {0, 1, 2}
B U C= {0, 1, 2, 3}

 Agora, podemos resolver o problema da seguinte forma:

          ( A U B) ∩  (B U C)={0, 1, 2}

Resposta: ( A U B) ∩  (B U C)={0, 1, 2}

Questão 3) Avaliando os conjuntos A={1, 2, 3} e B={2, 3, 5}, definimos o conjunto A-B como o conjunto que apresenta os elementos que pertencem a A e não a B. Portanto:

       A-B={1}

 Resposta: Item d

Questão 4) Gabarito da questão
a)V
b)V
c) F
d)V
e)F
f) V
g) F
h) F

Questão 5)  Considerando a questão e os conjuntos A={0, 1, 2, 3, 4, 5}, B={4, 5, 6, 7} e C={4, 5, 6, 8}, definiremos os seguintes conjuntos diferença:

*O primeiro conjunto representa todos os elementos que pertencem ao conjunto A e que não pertencem ao B.
A-B={0, 1, 2, 3}

* O segundo conjunto representa todos os elementos que pertencem ao conjunto B e  que não pertencem ao C
B-C={7}

Agora, o problema será solucionado da seguinte forma:

(A-B) ∩ (B-C) = {}

 Resposta: A intersecção entre A-B e B-C é vazia, portanto, não existe nenhum número comum aos dois conjuntos.

Agradecimentos:

Agradeço a todos que prestigiam a primeira postagem do meu novo blog. Espero que tenha ajudado alguém.
Quaisquer sugestões de melhorias no blog e de novos conteúdos, escrevam nos comentários. Se tiverem dúvida, escrevam também.
No dia 30 de outubro, lançarei a próxima postagem. 


Referências:





Postado por às Nenhum comentário:

quinta-feira, 4 de outubro de 2018

Tira-dúvidas: Sistemas de equação e de equações fracionárias

O que são sistemas de equações?

São um conjunto de equações que apresentam mais de uma incógnita. Para solucioná-las é necessário encontrar os valores que satisfaçam as duas equações. 
Um sistema de equações do primeiro grau é um sistema cujo o maior expoente das variáveis seja igual a 1.
Para encontrar os valores que que satisfaçam as equações, existem diversos métodos, mas somente serão citados os mais utilizados.
O par ordenado do sistema (x,y) sempre é a resposta do sistema.
Toda equação de primeiro grau em um sistema é escrita na forma: ax+by=c

Método de substituição

É um método no qual se  escolhe uma das equações e isola uma das variáveis para substituí-la na outra equação.

Exemplo:

 {x+y=60
 {5x-y=210

Isolando x na primeira equação temos que:

x+y=60
x=60-y

Substituindo na segunda equação:

5x-y=210
5(60-y)-y=210
300-5y-y=210
-5y-y=210-300
-6y=-90 

Multiplicando a equação por (-1)

-6y=-90(-1)
6y=90
y=90
     6

y=15


Agora que o valor de y foi determinado, pode-se substituir o valor de y em uma das equações.

x=60-y
x=60-15
x=45

Resposta: A solução do sistema é o par ordenado (45, 15). V={(45, 15)}

Método de adição:

Consiste na adição das duas equações de modo que a soma de uma das incógnitas se anule, permitindo a determinação da outra. Para que isso seja possível, precisamos multiplicar as equações ou apenas uma delas para que a soma de uma das variáveis seja zero.

Exemplo:

  {x+y=20
  {3x+4y=72

Multiplicando a primeira equação por (-3) temos que:

    {x+y=20 (-3)
    {3x+4y=72

Somando as duas equações, determinamos o valor de y
     {-3x-3y=-60
  +
     {3x+4y=72
               y=12

Como determinamos o valor de y, podemos substituí-lo em outra equação para determinar x.

    x+y=20
    x+12=20
     x=20-12
     x=8

Resposta: A solução do sistema é o par ordenado (8, 12). V={(8, 12)}

Sistema de equações fracionárias:

Sistema de equações fracionárias é aquele que possui frações algébricas, ou seja, possui variáveis no denominador. Para resolvê-las necessário simplificar as equações fracionárias para depois resolver as equações, pois assim, as operações com o sistema serão fáceis. Pode-se usar qualquer método para resolver as equações fracionárias.
Como o denominador de nenhuma equação pode ser zero, pois nenhum número pode ser dividido pelo mesmo, certas equações apresentarão restrições no conjunto universo de seus denominadores.

Exemplo:

{a+b=7
{   1   = 1         
{b-3     a-2            
   

Simplificando a segunda equação por meio do produto entre elas, já que é uma proporção, temos que:

1 (a-2)= 1 (b-3)
a-2=b-3
a-b= -3 +2
a-b= -1

Com a segunda equação simplificada, o sistema é:

{a+b=7
{a-b=-1

Usando o método de soma, temos que:

   {a+b=7
+
   {a-b=-1
     2a=6
        a=3

Substituindo o valor de a em uma das equações temos que:

  a+b=7
  3+b=7
   b=7-3
   b=4

Resposta: a=3; b=4

Dominando o conhecimento - Exercícios:

Questão 1) Solucione o sistema:

 {x+y=4
 {2x-3y=3

Questão 2) Solucione o sistema:

 {2x =y + 4
 { 3    2
 {x+y=48

Questão 3) Solucione o sistema:

{x+y=7
{  4  =6
{x-2   y

Questão 4) Solucione o sistema
{x + y= 7
{x - y= 5

Questão 5) Na compra de duas cadernetas e um caderno, Joana gastou R$ 13,00. Carlos comprou quatro cadernetas e três cadernos e gastou R$ 32,00. Determine o valor de uma caderneta e um caderno.              

Questão 6) Em um estacionamento, havia carros e motocicletas num total de 43 e 150 rodas. Calcule o número de carros e motos.                                         

Resolução:


Questão 1) 
{x+y=4
 {2x-3y=3

Isolando x na primeira equação temos que:

x+y=4
x=4-y

Substituindo na segunda equação:

2(4-y)-3y=3
8-2y-3y=3
-5y=3-8
-5y=-5

Multiplicando a equação por (-1)

-5y=-5 (-1)
5y=5
y=5
    5

y=1


Agora que o valor de y foi determinado, pode-se substituir o valor de y em uma das equações.

x=4-y
x=4-1
x=3

Resposta: O Par ordenado que satisfaz o sistema é (3,1).

Questão 2)

I)
 {2x =y + 4
 { 3    2
 {x+y=48


II)Igualando os denominadores da primeira equação, temos:

4x=3y+24
       6

4x=3y+24

4x-3y=24

III) {4x-3y=24
    {x+y=48

IV) Multiplicando-se a segunda equação por (3):
{4x-3y=24
 {x+y=48 (3)

V) Somando-se as duas equações determinaremos x:

 {4x-3y=24
  {3x+3y= 144
     7x=168
        x= 168
               7
         x=24

VI)Substituindo o valor de x na equação x+y=48, temos:

           24+y=48
           y=48-24
           y=24

Resposta: O par ordenado do siatema é (24, 24).


Questão 3)

{x+y=7
{  4  =6
{x-2   y

I) A segunda equação será simplificada para facilitar as contas

6(x-2)=4y
6x-12=4y
6x-4y=12 

II) Configurando o sistema:

{x+y=7
{6x-4y=12

III) Multiplicando a primeira equação por (4) temos:

 {x+y=7 (4)
{6x-4y=12

IV) Somando as duas equações, determinamos x

 {4x+4y=28
+
 {6x-4y=12
   10x=40
       x=40
           10

         x=4

V) Substituindo o valor de x na primeira equação do sistema ( x+y=7), obteremos o valor de y.

            4+y=7
             y=7-4
              y=3

Resposta: O Par ordenado que satisfaz o sistema é (4, 3). V={(4, 3)}.

 Questão 4)
{x + y= 7
{x - y= 5
I) Determinaremos o valor de x ao somarmos as duas equações.
  {x + y= 7
+
  {x - y= 5 
    2x= 12
       x= 12 
              2
         x= 6

II) Agora que o valor de x é conhecido, Determinaremos o valor de y substituindo o valor de x na primeira equação:
x + y= 7
* Sendo x= 6
6 + y= 7
y= 7 - 6
y= 1

Resposta: O Par ordenado que satisfaz o sistema é (6,1).

Questão 5) 
I) Analisando o problema, desenvolvemos os seguintes sistemas:
{2x + y= 13
{4x + 3y= 32

Onde
x: Preço de uma caderneta
y: Preço de um caderno

II) Agora, determinamos o valor de y na primeira equação para substituí-lo na segunda igualdade:
{2x + y= 13
{4x + 3y= 32

2x + y= 13
y= 13 - 2x

4x  + 3(13 - 2x)= 32
4x + 39 - 6x= 32
-6x + 4x= 32 - 39
-2x= -7
x=  7  
      2
x= 3,50

III) Agora que o valor de x é conhecido, basta substituí-lo em uma das equações para determinar o valor de y:

y= 13 - 2x
y= 13 - 2 • 3,5
y= 13 - 7
y= 6

 Resposta: Uma caderneta custa R$ 3,50 e um caderno custa R$ 6,00. 

Questão 6) 

I) Analisando o problema, desenvolvemos os seguinte sistema:
{x + y= 43
{4x + 2y=150

Onde
x: número de motocicletas
y:número de carros

II) Agora, determinamos o valor de y na primeira equação para substituí-lo na segunda igualdade:
{x + y= 43
{4x + 2y=150

x + y= 43
y= 43 - x

4x + 2(43 - x)= 150
4x + 86 - 2x= 150
4x - 2x=150 - 86
2x=64
x=  64  
       2
x= 32 carros

III) Agora que o valor de x é conhecido, basta substituí-lo em uma das equações para determinar o valor de y:

y= 43 - x
y= 43 - 32
y=11  motocicletas

Resposta: Haviam 32 carros e 11 motocicletas no estacionamento.                        


Agradecimentos:

Agradeço a todos que prestigiaram meu blog e espero que gostem das atuais e futuras postagens do blog. Essa postagem está fora do planejamento oficial do meu blog, porque está numa área de tira-dúvidas na qual tiro dúvidas de quais quer conteúdos de exatas. Quem não compreendeu algo da minha aula, comente.

Referências


Postado por às Nenhum comentário:
Assinar: Postagens (Atom)