Soma e diferença de dois arcos- demonstração geométrica

I) Demonstrações do seno da soma e diferença de dois arcos:

Em um triângulo qualquer, a área é igual ao semi produto de dois lados pelo seno do ângulo entre eles. Ou seja:

 

Fonte:http://pratico-e-basico.blogspot.com/2015/10/lei-dos-senos-e-cossenos.html

A= 1/2 • (b • c • sen Â) 

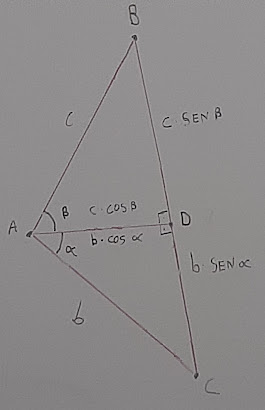
Logo, teremos as seguintes relações para os três triângulos da figura abaixo:

No triângulo ABC: A(ABC)= 1/2 • (b • c • sen (α + β))

No triângulo ABD: A(ABD)= 1/2 • (c • b • cos (α) • sen (β))

No triângulo ADC: A(ADC)= 1/2 •  (b • c • cos (β) • sen (α))

E sendo: A(ABC)= A(ABD) + A(ADC), temos:

1/2 • (b • c • sen (α + β))= 1/2 • (c • b • cos (α) • sen (β)) + 1/2 •  (b • c • cos (β) • sen (α))

Simplificando a expressão, temos:

sen (α + β)= cos (α) • sen (β) + cos (β) • sen (α)

Para encontrarmos o seno da diferença de dois ângulos, algumas propriedades das funções seno e cosseno serão necessárias. 

Sendo sen (-x)= -sen (x) e cos (-x)= cos (x), encontramos que:

sen (α + (-β))= cos (α) • sen (-β) + cos (-β)• sen (α)

sen (α - β)= cos (β) • sen (α) - cos (α) • sen (β)

II)Demonstrações do cosseno da soma e diferença de dois arcos:

Para demonstrarmos o cosseno da soma de dois arcos, aplicaremos a lei dos cossenos no triângulo ABC

[c • sen (β) + b • sen (α)]²= b² + c² - 2 • b • c • cos (α + β)

c² • sen² (β) + 2bc • sen (α) • sen (β) + b²• sen² (α)= b² + c² - 2bc • cos (α + β)

2bc • sen (α) • sen (β) + 2bc • cos (α + β)= b² - b² sen² (α) + c²- c² • sen² (β)

2bc • cos (α + β)= b²[1- sen² (α)] + c²[1- sen² (β)] - 2bc • sen (α) • sen (β)

2bc • cos (α + β)= b² cos² (α) + c² cos² (β) - 2bc • sen (α) • sen (β)

Dividindo ambos os membros por 2bc:

cos (α + β)= [b • cos² (α)]/2c + [c • cos² (β)]/2b - sen (α) • sen (β) (eq.i)

                        

Sendo c • cos (β)= b • cos (α), teremos:

b/c= cos (β)/cos (α) (eq.ii) 

c/b=cos (α)/cos (β) (eq.iii)  

Substituindo eq.ii e eq.iii em eq.i, teremos:

cos (α + β)= [cos (β) • cos (α)]/2 + [cos (α) • cos (β)]/2 - sen (α) • sen (β) 

cos (α + β)= cos (α) • cos (β) - sen (α) • sen (β) 

Para encontrarmos o cosseno da diferença de dois arcos, algumas propriedades das funções seno e cosseno serão necessárias. 

Sendo sen (-x)= -sen (x) e cos (-x)= cos (x), encontramos que:

cos (α + (-β))= cos (α) • cos (-β) - sen (α) • sen (-β) 

cos (α - β)= cos (α) • cos (β) + sen (α) • sen (β) 

Agradecimentos:

Agradecimentos:

Agradeço a todos que prestigiaram o meu blog e espero que gostem das atuais e futuras postagens. Quem tiver dúvidas, pode comentá-las. Espero ter ajudado, principalmente em meio a esta situação da pandemia.

Referências:

1-https://www.maxwell.vrac.puc-rio.br/24026/24026_4.PDF

2-http://pratico-e-basico.blogspot.com/2015/10/lei-dos-senos-e-cossenos.html