Semelhança de triângulos

Definição:

A semelhança de triângulos trata-se de uma relação estabelecida entre triângulos quando eles possuem lados proporcionais e ângulos congruentes. Ou seja, dois triângulos serão semelhantes se existir uma proporcionalidade entre os seus lados correspondentes e os seus ângulos forem congruentes. A semelhança entre dois triângulos é indicada por ~.

Entretanto, semelhança entre dois triângulos pode ser verificada de outras formas mais simples. Basta verificar se ela segue os casos de congruências abaixo:

Casos de semelhança:

Primeiro caso de semelhança-Caso ângulo-ângulo.

Dois triângulos serão semelhantes se apresentarem dois ângulos correspondentes iguais. Observe que, quando isso ocorre, o terceiro ângulo de ambos também será congruente. Isso é garantido pelo fato de que a soma dos ângulos internos de um triângulo sempre é 180 graus.
Logo, não é necessário verificar a proporção entre os lados homólogos (correspondentes) do triângulo. Na figura abaixo, encontra-se um exemplo desse tipo de semelhança.

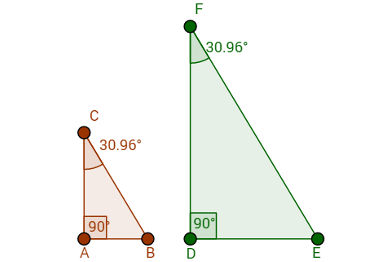
Fonte:https://brasilescola.uol.com.br/matematica/semelhanca-triangulos.htm

Segundo caso de semelhança- Critério Lado-Lado-Lado (LLL)

Dois triângulos serão semelhantes se apresentarem os seus lados homólogos (correspondentes) proporcionais. Logo, não é necessário verificar as medidas dos ângulos internos para observar que eles são semelhantes.
Na figura abaixo, encontra-se um exemplo desse caso de semelhança:

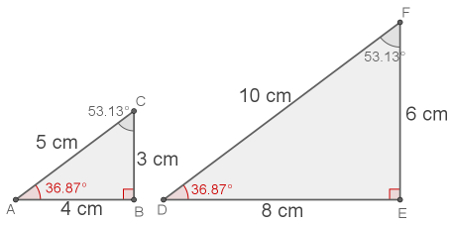
Fonte:https://brasilescola.uol.com.br/o-que-e/matematica/o-que-e-semelhanca-triangulos.htm
Nesse exemplo, observa-se que a razão entre os lados homólogos apresentam o mesmo resultado:

k= 10/5=6/3= 8/4 =2

Terceiro caso de semelhança-Critério Lado-Ângulo-Lado (LAL)

Se dois lados de um triângulo são proporcionais aos lados homólogos (correspondentes) do outro triângulo e o ângulo entre estes lados for congruente ao correspondente do outro, eles serão semelhantes.

Fonte:http://www.estudarmatematica.pt/2014/09/criterios-de-semelhanca-de-triangulos.html

Teorema fundamental da semelhança:

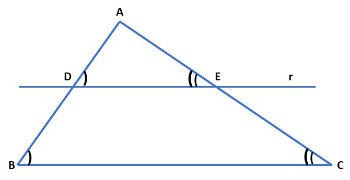
Quando uma reta paralela a um lado de um triângulo intercepta os outros dois em pontos distintos, forma-se um segundo triângulo semelhante ao primeiro.

Fonte:https://www.todamateria.com.br/semelhanca-de-triangulos/

Nessa figura acima, representamos o triângulo ABC e a reta r, paralela ao lado BC do triângulo ABC.

Ao observamos a figura, nota-se que os ângulos B e D são congruentes, assim como os ângulos C e Ê porque a reta r é paralela ao lado BC. Logo, os triângulos ABC e ADE são congruentes pelo critério de semelhança ângulo-ângulo (critério AA).

Razão entre os perímetros:

Se dois triângulos são semelhantes com uma razão de semelhança k, a razão entre os perímetros de dois triângulos semelhantes também é k.
Assim, sejam ∆ABC e ∆A'B'C' semelhantes, temos:
∆ABC ~ ∆A'B'C' => a/a'= b/b'= c/c'= k

Fonte da imagem:https://pt.wikipedia.org/wiki/Semelhan%C3%A7a_de_tri%C3%A2ngulos

Reescrevendo a proporção entre os lados:
a/a'= k => a=a' • k
b/b'= k => b= b' • k
c/c'=k => c= c' • k

Sabendo que o perímetro é a soma de todos os lados
P= a + b + c (perímetro de ∆ABC)
P'= a' + b' + c' (perímetro de ∆A'B'C')

A razão entre os perímetros será dada por:

P = a + b + c = a' • k + b' • k + c' • k = k • (a' + b' + c') = k
P' a' + b' + c' a' + b' + c' a' + b' + c'

Razão entre áreas:

A razão entre as áreas de dois triângulos semelhantes de razão k será k².

Fonte:https://pt.wikipedia.org/wiki/Semelhan%C3%A7a_de_tri%C3%A2ngulos

Assim, sejam ∆ABC e ∆A'B'C' semelhantes, temos:
∆ABC ~ ∆A'B'C' => a/a'= b/b'= c/c'= k

A área de ∆ABC será: AABC= (c • h)
2
A área de ∆A'B'C' será: AA'B'C'= (c' • h')/2

Dividindo a área do primeiro pela área do segundo:

   (c • h)
AABC  =   2 =   (c • h)   •    2 = c • h
AA'B'C'    (c' • h')   2 (c' • h') c' h'

2

Por semelhança entre os triângulos, obtém-se c/c'= k e h/h'= k.
Logo,

AABC = c • h = k • k= k²
AA'B'C'' c' h'

Exemplos:

Questão 1) Qual o valor de x nos triângulos a seguir

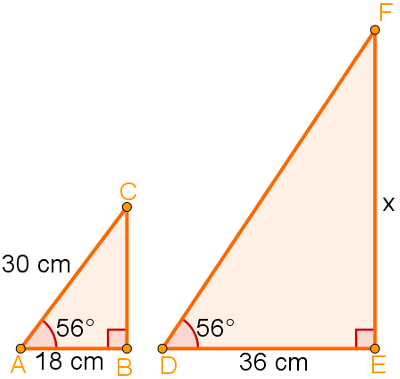
Fonte: https://brasilescola.uol.com.br/matematica/semelhanca-triangulos.htm
a) 48 cm
b) 49 cm
c) 50 cm
d) 24 cm
e) 20 cm

Resolução:
I) Primeiramente, observa-se que os triângulos ABC e DEF são semelhantes pelo critério ÂÂ. Contudo, o lado EF, de medida x, do triângulo maior é o lado correspondente do lado BC do triângulo menor, que apresenta medida desconhecida. Recorremos ao Teorema de Pitágoras para descobrir sua medida

BC² + 18²= 30²
BC² + 324= 900
BC²= 576 => BC= 24 m

II) Recorrendo a semelhança de triângulos para descobrir x, temos:

x/24= 36/18= 2
x/24= 2 => x= 48 cm

Resposta: Item a

Questão 2)Cefet/MG - 2015 A ilustração a seguir representa uma mesa de sinuca retangular, de largura e comprimento iguais a 1,5 e 2,0 metros, respectivamente. Um jogador deve lançar a bola branca do ponto B e acertar a preta no ponto P, sem acertar em nenhuma outra, antes. Como a amarela está no ponto A, esse jogador lançará a bola branca até o ponto L, de modo que a mesma possa rebater e colidir com a preta.

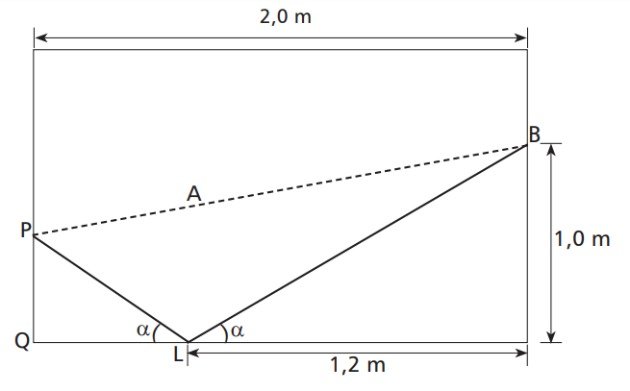
Questão Cefet-mg 2015 semelhança de triângulos

Fonte:https://www.todamateria.com.br/semelhanca-de-triangulos-exercicios/
Se o ângulo da trajetória de incidência da bola na lateral da mesa e o ângulo de rebatimento são iguais, como mostra a figura, então a distância de P a Q, em cm, é aproximadamente
a) 67
b) 70
c) 74
d) 81

Resolução:
I) Primeiramente, observa-se que os triângulos em vermelho são semelhantes pelo critério ÂÂ porque ambos possuem um ângulo reto e um ângulo de medida alfa.
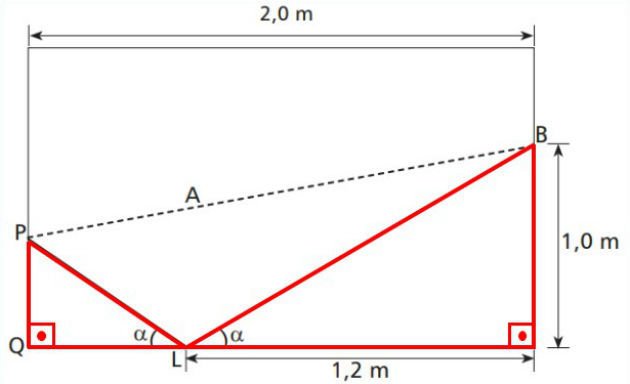
Questão cefet-MG 2015 semelhança de triângulos

Fonte:https://www.todamateria.com.br/semelhanca-de-triangulos-exercicios/

Sendo assim, podemos escrever a seguinte proporção:

PQ/1= 0,8/1,2
PQ= 0,67 m

PQ=67 cm

Resposta: Item a