Introdução:
O teorema de Pitágoras é um dos assuntos mais conhecidos na matemática, sendo muito abordado na geometria e na trigonometria. Por isso, ele é considerado um dos teoremas mais importantes da matemática. Ele fora desenvolvido pelo filósofo e matemático grego jônico Pitágoras de Samos
(570 a.c - 495 a.c).
Ele relaciona os lados de um triângulo retângulo e é enunciado da seguinte forma: "Em um triângulo retângulo, a soma dos quadrados dos seus catetos é igual ao quadrado da sua hipotenusa".
(570 a.c - 495 a.c).
Ele relaciona os lados de um triângulo retângulo e é enunciado da seguinte forma: "Em um triângulo retângulo, a soma dos quadrados dos seus catetos é igual ao quadrado da sua hipotenusa".
Fórmula:
De acordo com o enunciado do Teorema de Pitágoras, a sua fórmula é:
a²= b² + c²
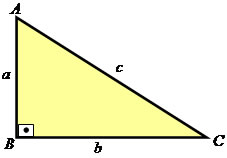
Onde
a- hipotenusa
b- cateto
c- cateto
a²= b² + c²

Onde
a- hipotenusa
b- cateto
c- cateto
Demonstração:
Vamos agora mostrar uma das diversas formas de encontrar a fórmula do Teorema de Pitágoras. Para isso, considere um quadrado ABCD cujo lado mede (b + c), tal como na figura abaixo.
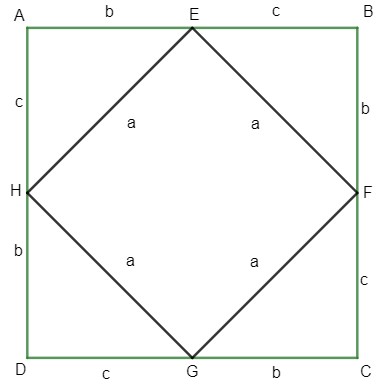
-Primeiramente, mede-se a área do quadrado ABCD
AABCD = (b + c)²= b² + 2bc + c²
-Depois, mede-se a área do quadrado EFGH
AEFGH = a²
-Agora, é possível observar que existem quatro triângulos congruentes cuja área é:
Atriângulo= b • c
2
Determinadas estas áreas, deve-se calcular a área do quadrado EFGH em função das áreas do quadrado ABCD e dos quatro triângulos. Veja que, se retirarmos as áreas dos triângulos da área do quadrado ABCD, sobra apenas a área do quadrado ABCD. A partir disso, obtém-se:
AEFGH = AABCD - 4Atriângulo
a²= b² + 2bc + c² - 4 • b • c
Determinadas estas áreas, deve-se calcular a área do quadrado EFGH em função das áreas do quadrado ABCD e dos quatro triângulos. Veja que, se retirarmos as áreas dos triângulos da área do quadrado ABCD, sobra apenas a área do quadrado ABCD. A partir disso, obtém-se:
AEFGH = AABCD - 4Atriângulo
a²= b² + 2bc + c² - 4 • b • c
2
a²= b² + 2bc + c² - 2bc
a²= b² + c²

Resolução:
A medida x corresponde a hipotenusa deste triângulo e os outros dois lados correspondem aos seus catetos. Recorrendo ao Teorema de Pitágoras, obtém-se:
x²= 6² + 8²
x²= 36 + 64
x²= 100
x= √(100)
x= 10 cm
Resposta: x= 10 cm
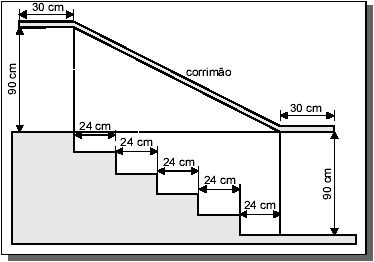
Exemplo 2:(ENEM). Na figura abaixo, que representa o projeto de uma escada de 5 degraus de mesma altura, o comprimento total do corrimão é igual a:
a²= b² + 2bc + c² - 2bc
a²= b² + c²
Exemplos:
Exemplo 1: Determine a medida x no triângulo retângulo abaixo:
Resolução:
A medida x corresponde a hipotenusa deste triângulo e os outros dois lados correspondem aos seus catetos. Recorrendo ao Teorema de Pitágoras, obtém-se:
x²= 6² + 8²
x²= 36 + 64
x²= 100
x= √(100)
x= 10 cm
Resposta: x= 10 cm
Exemplo 2:(ENEM). Na figura abaixo, que representa o projeto de uma escada de 5 degraus de mesma altura, o comprimento total do corrimão é igual a:

A) 1,8 m. B) 1,9 m. C) 2,0 m. D) 2,1 m E) 2,2 m.
Resolução:
I) Observe que a altura entre o primeiro degrau e o corrimão é de 90 cm. Somando o comprimento de cada degrau, obtém-se que 5 • 24= 120 cm.
II) A partir do Teorema de Pitágoras, obtém-se que o comprimento total do corredor medirá:
a²= b² + c²
a²= 90² + 120²
a²= 8100 + 14400
a²= 22500
a=√(22500)
a= 150 cm
III) Visto que o corrimão apresenta dois pedaços que medem 30 cm, obtém-se que o seu comprimento total será:
L= 150 + 30 + 30
L= 210 cm
Resposta: Item D.
2-https://www.todamateria.com.br/teorema-de-pitagoras/a²= 90² + 120²
a²= 8100 + 14400
a²= 22500
a=√(22500)
a= 150 cm
III) Visto que o corrimão apresenta dois pedaços que medem 30 cm, obtém-se que o seu comprimento total será:
L= 150 + 30 + 30
L= 210 cm
Resposta: Item D.
Agradecimentos:
Agradeço a todos que prestigiaram o meu blog e espero que gostem das atuais e futuras postagens. Quem tiver dúvidas, pode comentá-las. Espero ter ajudado.
Referências:
3-https://www.infoescola.com/matematica/teorema-de-pitagoras/
4-https://www.educamaisbrasil.com.br/enem/matematica/teorema-de-pitagoras
5-https://alunosonline.uol.com.br/matematica/trigonometria-no-triangulo-retangulo.html
6-https://educador.brasilescola.uol.com.br/estrategias-ensino/demonstracoes-teorema-pitagoras.htm
7-https://matematicabasica.net/teorema-de-pitagoras/
8-https://pt.wikipedia.org/wiki/Pit%C3%A1goras
Nenhum comentário:
Postar um comentário