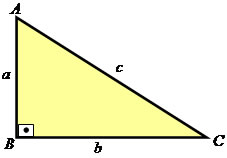
3a = 7c e 3b = 8c
a) 30°
b) 60°
c) 45°
d) 120°
e) 135°
Resolução:
I) Utilizando as relações dadas pela questão, teremos;
* 3a=7c
a= 7c/3
*c=c
*3b= 8c
b=8c/3
II) Chamando o ângulo oposto ao lado a de α, aplicaremos a lei dos cossenos para determinar o valor do ângulo α:
a²= b² + c² - 2 • b • c • cos α
(7c/3)²= (8c/3)² + (c)² - 2 • (8c/3) • (c) • cos α
49c²/9= 64c²/9 + c² - 16c² • cos α/3
49c²/9= 64c²/9 + c² - 16c² • cos α/3
III) Multiplicando ambos os lados da equação por nove, teremos
9 • (49c²/9)= (64c²/9 + c² - 16c²• cos α/3) • 9
49c²= 64c² + 9c² - 48c² • cos α
49c²= 73c² - 48c² • cos α
48c² • cos α= 73c² - 49c²
48c² • cos α= 24c²
cos α= 24c²/48c²
cos α= 1/2 => α=60°
Resposta:Item b
Desafio 2 - (ITA) Seja α um número real tal que α > 2(1 + √2) e considere a equação
x² − αx + α + 1 = 0. Sabendo que as raízes reais dessa equação são os cotangentes de dois dos ângulos internos de um triângulo, então o terceiro ângulo interno desse triângulo vale:
a) 30°
b) 45°
c) 60°
d) 135°
e) 120°
Resolução:
I) Sabendo que os cotangentes de dois dos ângulos internos deste triângulo, que aqui serão representados por a e b, são as raízes desta equação, teremos que a soma e produto desta equação serão:
x² − αx + α + 1 = 0
* Soma das raízes
cotg a + cotg b= - (-α)
1
cotg a + cotg b= α
* Produto das raízes
cotg a • cotg b= α + 1
1
cotg a • cotg b= α + 1
II) Aplicando a cotangente da soma de dois arcos, teremos:
cotg (a + b)= (cotg a • cotg b) - 1
cotg a + cotg b
cotg (a + b)= α + 1 - 1
α
cotg (a + b)= α
α
cotg (a + b) = 1
Como (a + b) < 180°, temos que:
cotg (a + b) = 1 => a + b= 45°
III) Lembrando-se de que a soma dos ângulos internos de um triângulo é igual 180° , teremos que o terceiro ângulo interno ( sendo este ângulo representado por c) será:
a + b + c= 180°
45° + c= 180°
c= 180° - 45°
c= 135°
Resposta: Item e.
Desafio 3 - (ITA) (ITA) Num triângulo isósceles, o perímetro mede 64 m e os ângulos adjacentes são iguais ao arc cos 7/25. Então a área do triângulo é de:
a) 168 m²
b) 192 m²
c) 84 m²
d) 96 m²
e) 157 m²
Resolução:
I) Primeiramente, devemos relacionar os lados deste triângulo sabendo que dois deles são iguais e que o perímetro do triângulo, ou a soma das medidas de todos os seus lados, é igual a 64 metros. Escreveremos os lados desta figura como a e b.
P= 64 m
a + a + b= 64
b= 64 - 2a
b= 2 • (32 - a)
II) A questão diz que os ângulos adjacentes (os da base), que serão escritos como α, são iguais a
arc cos 7/25. Isso significa que cos α= 7/25. Com isso e a relação entre os lados deste triângulo, determinaremos os lados deste triângulo através da Lei dos Cossenos.
a²= a² + b² - 2 • a• b • cos α
a² - a²= b² - 2 • a• b • cos α
0= b² - 2 • a• b • cos α
2 • a• b • cos α= b²
-Dividindo ambos os lados da equação por b, teremos:
2a • cos α= b
2a • 7/25 = b
14a/25 = b
14a= 25b
14a= 25 • 2 • (32 - a)
14a= 50 • (32 - a)
14a= 1600 - 50a
14a + 50a= 1600
64a= 1600
a= 1600/64
a= 25 metros
-Descoberta a medida do lado a, determinaremos quanto medem os lados b.
b= 2 • (32 - a)
b= 2 • (32 - 25)
b= 2 • 7
b= 14 metros
IV) Agora, determinaremos sen α através da relação fundamental da trigonometria para facilitar o cálculo da área deste triângulo.
sen² α + cos² α= 1
sen² α= 1 - cos² α
sen² α= 1 - (7/25)²
sen² α= 1 - 49/625
sen² α= (625 - 49)/625
sen² α= 576/625
sen α=√(576/625)
sen α= 24/25
V) Tendo conhecimento das medidas dos lados deste triângulo e de sen α, basta determinar a área deste triângulo.
A= a • b • sen α
2
A= 25 • 14 • 24
2 25
A= 8400
50
A= 168 m²
Resposta: A= 168 m². Item a
sen α= 24/25
V) Tendo conhecimento das medidas dos lados deste triângulo e de sen α, basta determinar a área deste triângulo.
A= a • b • sen α
2
A= 25 • 14 • 24
2 25
A= 8400
50
A= 168 m²
Resposta: A= 168 m². Item a
Agradecimentos:
Agradeço a todos que prestigiaram o meu blog e espero que gostem das atuais e futuras postagens. Quem tiver dúvidas, pode comentá-las. Espero ter ajudado.