Questão 1)
Questão 2)
Questão 3)
Questão 4)
Questão 5)
Questão 6)
Resoluções:
Questão 1)
RAB= R + [(R•RAB)/(RAB + R)]
RAB - R=(R•RAB)/(RAB + R)
(RAB - R) • (Rab + R)= (R•RAB)
RAB² - R² = R•RAB
RAB² -R•RAB - R²= 0
Resolvendo a equação quadrática:
∆=b² - 4ac
∆=R² - [4 • 1 • (-R²)]
∆=5R²
RAB= (R ± R√5)/2 e RAB> 0
Assim,
RAB= R(1 + √5)/2
Resposta: Item D
Questão 2)
I) Forças em B:
sen α= Fcp/T=mω²r/T => T • sen α=mBω²r (i)
cos α= PB/T =mBg/T => T • cos α = mBg (ii)
II) Forças em A:
NA + T • sen α= PA = mA • g (iii)
T • cos α+ Fat= Fel= kx (iv)
Fat=μNA (v)
III)
Isolando NA em (iii) e substituindo (i) em (iii).
NA + T • sen α= mA • g
NA = mA • g - T • sen α
NA = mA • g - mBω²r (vi)
IV) Substituindo (vi), (v) e (ii) em (iv)
T • cos α+ Fat= Fel= kx
mBg +μ(mA • g - mBω²r)=kx => x= [mBg +μ(mA • g - mBω²r)]/k
Resposta: x= [mBg +μ(mA • g - mBω²r)]/k
Questão 3)
I) Visto que o enunciado afirma que os blocos não possuem movimento relativo entre si, a análise das forças em apenas um dos blocos será suficiente para a determinação da velocidade angular mínima.
Forças:
N • sen θ - Fat • cos θ= Fcp= mω²r (i)
N • cos θ + Fat • sen θ= P= mg (ii)
Fat=μN (iii)
II) Isolando a força normal (N) e substituindo (iii) em (i), têm-se:
N • sen θ - Fat • cos θ= mω²r
N • sen θ - μN • cos θ= mω²r
N • (sen θ - μ • cos θ)= mω²r
N=(mω²r)/(sen θ - μ • cos θ) (iv)
III)Isolando a força normal (N) e substituindo (iii) em (ii), têm-se:
N • cos θ + Fat • sen θ= mg
N • cos θ + μN • sen θ= mg
N • (cos θ + μ • sen θ)= mg
N=(mg)/(cos θ + μ • sen θ) (v)
IV) Igualando (iv) e (v)
N=N
(mω²r)/(sen θ - μ • cos θ) = (mg)/(cos θ + μ• sen θ)
Simplificando
(ω²r)/(sen θ - μ cos θ)= g/(cos θ + μ • sen θ)
ω²=(g/r) • [(sen θ - μ • cos θ)/(cos θ + μ • sen θ)]
ω=√{(g/r) • [(sen θ - μ • cos θ)/(cos θ + μ • sen θ)]}
Resposta: Item d -√{(g/r) • [(sen θ - μ • cos θ)/(cos θ + μ • sen θ)]}.
Questão 4)
I) Considerando que o bloco inicia e termina sua trajetória com velocidade nula, infere-se que a variação de energia cinética é nula. Pelo teorema da energia cinética, têm-se:
τR=ΔEc= τF.elétrica + τF.elástica + τFat + τP
ΔEc=0= τF.elétrica + τF.elástica + τFat + τP
h= d • sen θ=
II)Substituindo os trabalhos realizados, obtém-se:
0= QV + (kx²/2) - (μ • m • g •d • cos θ) - (m • g •d • sen θ)
d • mg • (μ • cos θ + sen θ)=QV + (kx²/2)
Multiplicando ambos os lados da igualdade por 2
2d • mg • (μ • cos θ + sen θ)= 2QV + kx²
d= (2QV + kx²)/[2mg(μ • cos θ + sen θ)]
Resposta: Item E - d= (2QV + kx²)/[2mg(μ • cos θ + sen θ)]
Questão 5)
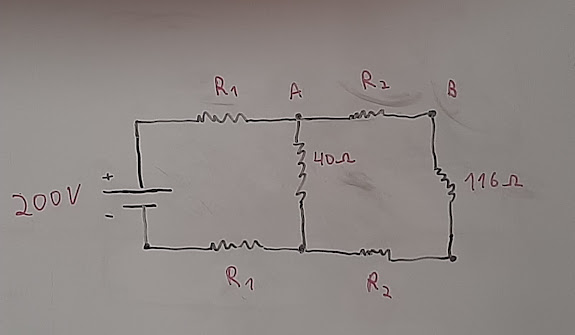
I) Visto que os fios mencionados possuem certa resistividade ( ρ=0,4Ω mm²/m), é possível tratá-los como resistores de resistências R1 e R2 como na figura abaixo:
R1= ρ • (L1/A)
R1=0,4 • (25/2)= 5 Ω
R2=ρ • (L2/A)
R2=0,4 • (10/2)= 2 Ω
II) Conhecidas às resistências do circuito, calcularemos sua resistência equivalente para se calcular a corrente total do circuito
Req= {[(116 + 2 + 2) • 40]/[(116 + 2 +2 + 40)]} + 5 + 5
Req={[120 • 40]/160} + 10
Req= 40 Ω
Pela segunda Lei de Ohm
Ueq= Req • i
200=40i => i= 5 A
III) DDP entre A e B
A corrente do circuito é divida do modo mostrado na imagem abaixo:
Resistência equivalente AD (Trecho em paralelo)
RAD= {[(116 + 2 + 2) • 40]/[(116 + 2 +2 + 40)]}= 30 Ω
UAD = RAD • i
UAD = 30 • 5= 150 V
Pela primeira Lei de Ohm no trecho em série ABCD (RABCD=2 +2 + 116= 120 Ω) , teremos:
UAD = RABCD • i(AB)=> 150= 120 • i(AB) =>i(AB) = 150/120
i(AB) = 150/120= 5/4= 1,25 A
i(AB)= 1,25 A
Por fim, obtêm-se:
UAB= RAB • i(AB)
UAB= 2 • 1,25
UAB= 2,5 V
Resposta: Item B
Questão 6)
I) Velocidade de máxima oscilação do conjunto (Vmáx)
Do MHS, obtêm-se:
Vmáx= ωA
Vmáx= 2 • 0,4=0,8 m/s
II) Colisão de m com M
Sabe-se que a colisão é perfeitamente inelástica e, com isso, teremos?
Q(M +m)= Q(M) + Q(m)
(M +m) • Vmáx= M • 0 + m • Vo
(10 + 2) • 0,8= 2 •Vo => Vo= 4,8 m/s
Resposta: Item d. Vo= 4,8 m/s
Novidade:
Abri um server no discord para tirar dúvidas dos leitores do blog de várias matérias (de exatas claro, kkkkkk). Espero que gostem. Link:https://discord.gg/ZShrt7jxru
Agradecimentos:
Agradeço a todos que prestigiaram o meu blog e espero que gostem das atuais e futuras postagens.
Quem tiver dúvidas, pode comentá-las. Espero ter ajudado, principalmente em meio a esta situação da pandemia.