Introdução:
A famosa fórmula do Teorema de Pitágoras é de conhecimento geral da maioria dos estudantes do ensino médio e fundamental II, mas nem todas as suas aplicações na geometria plana são conhecidas. Agora, algumas delas serão apresentadas porque este teorema tem muitas aplicações e não seria possível apresentar todas em única postagem. Por isso, apresentaremos somente algumas das mais importantes e usuais na matemática.
Diagonal do quadrado:
Para determinarmos a diagonal de um quadrado, precisamos levar em consideração o fato de que este segmento divide o quadrado em dois triângulos. Portanto, podemos utilizar o Teorema de Pitágoras para determinar a diagonal de um quadrado a partir do seus lados. Com estas informações descobrimos a partir do Teorema de Pitágoras que a medida da diagonal do quadrado é:
d^2= 2L²
d=√2L²
d=L√2
Exemplo: Determine a medida da diagonal de um quadrado cujos lados medem 8 cm.
* Visto que a medida do lado deste quadrado é conhecido, basta substituí-la na fórmula da diagonal do quadrado.
d=L√2
d= 8√2 cm
d=L√2
Exemplo: Determine a medida da diagonal de um quadrado cujos lados medem 8 cm.
* Visto que a medida do lado deste quadrado é conhecido, basta substituí-la na fórmula da diagonal do quadrado.
d=L√2
d= 8√2 cm
Resposta: d= 8√2 cm
Altura do triângulo equilátero:
Neste tipo de triângulo, a altura divide o triângulo em dois triângulos retângulos menores cujas bases são L/2.
Para encontrarmos o valor correspondente a altura do triângulo equilátero, aplicaremos o Teorema de Pitágoras, o que determina que:
L^2= h^2 +(L/2)²
L^2=h^2 + L² => h^2= L^2 - L²
4 4
h^2= 3L²
4
h= √3L² = √3 •√L²
√4 √4
h= √3L² = √3 •√L²
√4 √4
h= L√3
2
Exemplo: Determine a altura de um triângulo equilátero cujos lados medem 10 cm.
* Visto que a medida do lado deste triângulo equilátero é conhecida, basta substituí-la na fórmula da altura do triângulo equilátero.
h= L√3
2
h= 10√3
2
h= 5√3 cm
Resposta: h= 5√3 cm
h= L√3
2
h= 10√3
2
h= 5√3 cm
Resposta: h= 5√3 cm
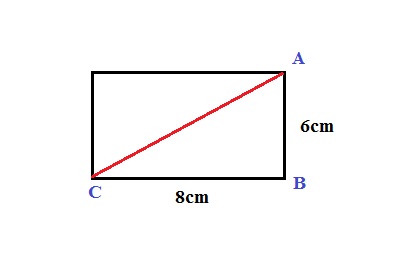
Diagonal do retângulo:
A diagonal d de um retângulo de lados a e b pode ser facilmente calculada a partir do Teorema de Pitágoras, pois ela divide o retângulo em dois triângulos retângulos idênticos, correspondendo a hipotenusa de cada um deles.
Assim temos que:
d²= a² + b²
Exemplo: Determine a diagonal de um retângulo cujos lados medem 8 cm e 6 cm.
*Visto que as medidas do retângulo são conhecidas, a diagonal desta figura medirá:
d²= a² + b²
d²= 8² + 6²
d²= 64 + 36
d²= 100
d=√100
d= 10 cm
Resposta: A diagonal deste retângulo mede 10 cm.
d²= 8² + 6²
d²= 64 + 36
d²= 100
d=√100
d= 10 cm
Resposta: A diagonal deste retângulo mede 10 cm.



 Fonte:
Fonte: