Introdução:
A geometria espacial é um ramo da matemática que foca no estudo das figuras tridimensionais, ou seja, aquelas que apresentam largura, comprimento e altura. Ela estuda sólidos geométricos como o cubo, cilindro, cone, prisma e a esfera.
A área superficial destes objetos é obtida pela soma das áreas de cada figura geométrica que os compõem, que pode ser obtida pela planificação deles e por fórmulas específicas para cada sólido.
Apresentaremos algumas fórmulas para o cálculo da área de alguns sólidos geométricos e como aplicá-las.
Apresentaremos algumas fórmulas para o cálculo da área de alguns sólidos geométricos e como aplicá-las.
Cubo:
Tipo especial de paralelogramo nos quais todas as suas arestas e faces são congruentes. Ele é um poliedro regular com 8 vértices e 12 arestas.
Sua área é dada por:
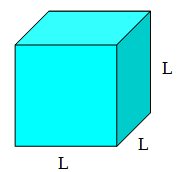
Cubo com medidas L.
Fonte: https://www.infoescola.com/matematica/volume-do-cubo-e-paralelepipedo/
A= 6 • L²
* Exemplo: Qual a área de um cubo cujo lado mede 4 cm ?
I) Como conhecemos a medida do lado deste cubo, basta substituí-lo na fórmula para determinamos sua área.
A=6 • L²
A=6 • 4²
A=6 • 16
A= 96 cm²
Paralelepípedo:
Figura geométrica tridimensional que é definida como um prisma cujo as faces são paralelogramos. Ele apresenta seis faces, 12 arestas e 8 vértices.
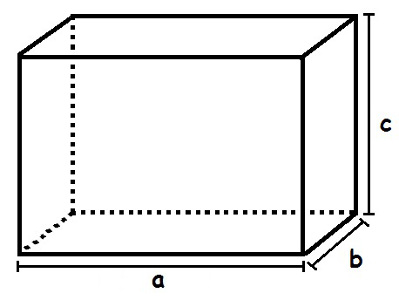
Fonte:https://brasilescola.uol.com.br/matematica/volume-paralelepipedo-cubo-cone.htm
Área total do paralelepípedo:
A=2 • (ab + ac + bc)
*Exemplo: Qual a área de um bloco retangular que apresenta medidas de comprimento e largura iguais a 30 cm e uma altura com medida igual a 15 cm.
I) Como o comprimento e a largura são iguais, temos que a= 30 cm e b= 30 cm. Como a altura mede 15 cm, temos que a área deste paralelepípedo será:
A= 2 • ( 30 •30 + 30 • 15 + 30 • 15)
A= 2 • ( 900 + 450 + 450)
A= 2 • (900 + 900)
A= 2 • 1800
A= 3600 cm²
I) Como o comprimento e a largura são iguais, temos que a= 30 cm e b= 30 cm. Como a altura mede 15 cm, temos que a área deste paralelepípedo será:
A= 2 • ( 30 •30 + 30 • 15 + 30 • 15)
A= 2 • ( 900 + 450 + 450)
A= 2 • (900 + 900)
A= 2 • 1800
A= 3600 cm²
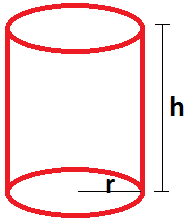
Cilindro:
O cilindro é uma figura geométrica com formato circular que apresenta o mesmo diâmetro em todo o seu comprimento. Ele é composto por duas bases circulares dispostas em planos distintos e perpendiculares e todos os pontos entre eles.
Ele apresenta os seguintes elementos:
Raio: Distância entre o centro e uma extremidade do cilindro. (r)
Base: O cilindro apresenta uma base superior e inferior. Ambas são circulares, paralelas entre si e congruentes.
Geratriz: Segmento que passa de uma base para a outra. Corresponde a altura do cilindro.(altura h=g)
Diretriz: Corresponde aos pontos da geratriz nas extremidades do cilindro.
Um cilindro pode ser classificado como:
Reto: Cilindro cuja geratriz é perpendicular às bases e congruente a altura h.
Oblíquo: Cilindro cuja geratriz não é perpendicular as bases e que apresenta uma medida não congruente a da altura.
Equilátero: Cilindro cuja altura igual a medida do raio, ou seja, o que apresenta uma altura 2r.
* Área da base:
Ab= πr²
A= Área lateral
Al= 2πrh
* Área total
At=2 Ab + Al
At= 2πr(r + h)
* Exemplo: Calcule a área de um cilindro cujo altura mede 20 cm e o diâmetro é igual a 8 cm.
I) Primeiramente devemos que o raio de um círculo corresponde a metade do seu diâmetro (d=r/2), logo r=8/2= 4 cm. Visto isso, podemos substituir os valores para aplicá-los na fórmula.
At= 2πr(r + h)
At= 2 • π • 4 • (4 + 20)
At=8π • (24)
At=192π cm²
Ab= πr²
A= Área lateral
Al= 2πrh
* Área total
At=2 Ab + Al
At= 2πr(r + h)
* Exemplo: Calcule a área de um cilindro cujo altura mede 20 cm e o diâmetro é igual a 8 cm.
I) Primeiramente devemos que o raio de um círculo corresponde a metade do seu diâmetro (d=r/2), logo r=8/2= 4 cm. Visto isso, podemos substituir os valores para aplicá-los na fórmula.
At= 2πr(r + h)
At= 2 • π • 4 • (4 + 20)
At=8π • (24)
At=192π cm²
Esfera:
Figura tridimensional formada por um conjunto de pontos que podem estar a uma distância do seu centro igual ou menor que o seu raio R.

Fonte:https://matematicabasica.net/area-da-esfera/
Fórmula:
At=4πR²
* Exemplo: Calcule a área de uma esfera que apresenta um raio igual a 10 cm.
At= 4 • π • 10²
At= 4 • π • 100
At= 400 • π
At= 400π cm²
Cone:
Cone é uma figura geométrica que apresenta uma base circular constituída por segmentos de reta que apresentam como extremidade um vértice comum.
A altura do cone é a distância do plano da base até o vértice do cone. Esta figura possui a geratriz, ou seja, qualquer segmento formado por uma extremidade no vértice e outra na base da figura.
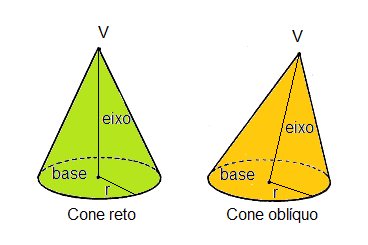
-Cone oblíquo: É o que possui o eixo não é perpendicular a base, ou seja, a altura e a base formam um ângulo de 90 graus:
-Cone reto: Apresenta um eixo perpendicular a base, ou seja, a altura e a base são perpendiculares e a geratriz do cone é dada pelo Teorema de Pitágoras a partir da seguinte relação: g^2= r^2 + h^2.
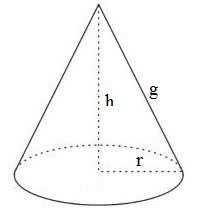
Fonte:https://www.todamateria.com.br/volume-do-cone/

Fonte:https://www.todamateria.com.br/volume-do-cone/
Para calcular a base do cone, aplicamos a seguinte fórmula:
* Área da base
Ab= πr²
Para a área lateral do cone, aplicamos outra fórmula
*Área lateral
Al= πrg
A área total do cone será dada pela soma da lateral e da base.
* Área total
At= Ab + Al
At= πr² + πrg
At= πr(r + g)
* Exemplo: Qual a área total e lateral de um cone que possui altura igual a 12 cm e raio da base igual a 5 cm
I) Primeiramente, devemos calcular a geratriz do cone:
g²= r² + h²
g²=5² + 12²
g²= 25 + 144
g²= 169
g=√169
g=13 cm
II) Visto que agora determinamos a geratriz, podemos calcular a área lateral e total do cone substituindo os valores das medidas do mesmo nas fórmulas. Com isso temos os seguintes resultados
* Área lateral
Al= πrg
Al= π • 5 • 13
Al= 65π cm²
*Área total
At= πr(r + g)
At= π • 5 • (5+ 13)
At= π • 5 • 18
At= 90π cm²
Agradecimentos:
Referências:
2-https://www.infoescola.com/matematica/area-externa-de-solidos-geometricos/
3-https://www.infoescola.com/matematica/volume-de-solidos-geometricos/exercicios/
4-http://www.matematicadidatica.com.br/Solidos-Geometricos-Exercicios-Calculo-Area-Volume.aspx
5-https://exercicios.brasilescola.uol.com.br/exercicios-matematica/exercicios-sobre-solidos-geometricos.htm
6-http://questoesdevestibularnanet.blogspot.com/2013/11/questoes-resolvidas-de-vestibular-sobre.html
7-https://exercicios.mundoeducacao.bol.uol.com.br/exercicios-matematica/exercicios-sobre-area-esfera.htm
8-http://www.profcardy.com/exercicios/lista.php?a=geometria%20espacial
9-https://escolaeducacao.com.br/geometria-espacial/
10-https://matematicabasica.net/area-do-cilindro/
11-https://www.todamateria.com.br/cone/
12-https://www.todamateria.com.br/area-do-cone/
13-https://matematicabasica.net/cilindro/
14-https://www.todamateria.com.br/area-do-cilindro/
15-http://www.matematiques.com.br/conteudo.php?id=554
3-https://www.infoescola.com/matematica/volume-de-solidos-geometricos/exercicios/
4-http://www.matematicadidatica.com.br/Solidos-Geometricos-Exercicios-Calculo-Area-Volume.aspx
5-https://exercicios.brasilescola.uol.com.br/exercicios-matematica/exercicios-sobre-solidos-geometricos.htm
6-http://questoesdevestibularnanet.blogspot.com/2013/11/questoes-resolvidas-de-vestibular-sobre.html
7-https://exercicios.mundoeducacao.bol.uol.com.br/exercicios-matematica/exercicios-sobre-area-esfera.htm
8-http://www.profcardy.com/exercicios/lista.php?a=geometria%20espacial
9-https://escolaeducacao.com.br/geometria-espacial/
10-https://matematicabasica.net/area-do-cilindro/
11-https://www.todamateria.com.br/cone/
12-https://www.todamateria.com.br/area-do-cone/
13-https://matematicabasica.net/cilindro/
14-https://www.todamateria.com.br/area-do-cilindro/
15-http://www.matematiques.com.br/conteudo.php?id=554
Nenhum comentário:
Postar um comentário