Exatas para todos - Ensino de qualidade em quantidade: setembro 2018

O que são?

Primeiramente, um conjunto é a reunião de elementos com características comuns. Considerando os números como elementos, temos os conjuntos numéricos. Por convenção, quando representamos um por extenso, precisamos escrever os elementos dentro de chaves {}. Se o conjunto for infinito, apresentará infinitos números e, para representar isso, utilizamos reticências (os conhecidos três pontinhos).

Existem cinco conjuntos que são fundamentais para o estudo da matemática como um todo porque são mais utilizados em problemas do cotidiano como o cálculo da área de um terreno, a construção de um prédio e entre outros. Estes conjuntos são:

Números naturais:

Conjunto representado pela letra N, sendo composto por todos os números positivos e o zero. Surgiu quando o ser humano logo desenvolveu a matemática com a necessidade de contar e medir tudo ao seu redor. Escrevendo este conjunto por extenso, temos:

N={0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ...}

Para representar os números naturais diferentes de zero, ou não nulos, escrevemos N*. Ele é escrito por extenso como:

N*={1, 2, 3, 4, 5, 6, 7, 8, 9, 10...}

Este conjunto é bastante utilizado em todas as áreas da matemática e das ciências que a utilizam.

Números inteiros:

Conjunto representado pela letra Z, inclui os números inteiros negativos, positivos e o zero. Surgiu quando as pessoas precisavam expressar dívidas ou perdas. Ele é escrito como:

Z={... -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5...}

Existem subconjuntos dos números inteiros que são:

Inteiros não negativos: Representado pelos números inteiros positivos e o zero.

Z+={0, 1, 2, 3, 4, 5, 6, 7...}

Inteiros não negativos e não nulos: Números inteiros positivos e diferentes de zero

Z*+={1, 2, 3, 4, 5, 6, 7, 8 ...}

Inteiros não positivos: Constituído por números inteiros negativos e o zero.

Z_={... -5, -4, -3, -2, -1, 0}

Inteiros não positivos e não nulos: Representado somente pelos números negativos e diferentes de zero.

Z*_={... -6, -5, -4, -3, -2, -1}

Como pode-se observar, o conjunto dos números inteiros contém o conjunto dos números naturais.

Números racionais:

Conjunto constituído por: todos os números naturais e inteiros; as frações; os decimais; as dízimas periódicas, pois podem ser escritas em frações.

Ser um número racional significa que ele é um número que pode ser escrito pelo quociente entre dois inteiros p/q desde que seja diferente de zero. Este conjunto é representado pela letra Q. Surgiu quando a matemática se tornou mais precisa, principalmente, por causa da necessidade de muitos de realizarem contas cada vez mais exatas.

Ele é escrito como:

Q={-0,4; -2/9; 0; 1/4; 2; 3,333...}

Assim como o conjunto dos números inteiros, o dos números apresentam também diversos subconjuntos que são:

Os racionais não negativos: Representado por Q+, é constituído pelos números racionais positivos e o zero.

Q+={0, 0,4; 1/2, 9/4...}

Os racionais não negativos: Representado por Q-, é constituído pelos números racionais negativos e o zero.

Q-={-0,125; -1,3;-1/4, -2/5, 0...}

Racionais não negativos não nulos: Constituídos pelos números racionais positivos, excluindo o zero.

Q*+={4/5, 3/2, 7,2; 4,5...}

Racionais não positivos não nulos: Constituídos pelos números racionais negativos, excluindo o zero.

Q*-={-4/5, -3/2, -7,2; -4,5...}

Números irracionais:

É um conjunto que não pertence aos naturais, inteiros e racionais. Constitui-se de números que apresentam forma decimal infinita e não periódica. Entende-se período como a repetição de uma mesma sequência numérica, como nas dízimas periódicas. São representados pela letra I.

Exemplos:

π=3,1459265...
Raízes de números não exatas, como a raiz quadrada de 2=1,4142135...
e=2,718...

Números reais:

Conjunto que engloba todos os números naturais, inteiros, racionais e irracionais. É representado pela letra R.

R={...-π, 0 , 1, 2/3, e, 3,3...}

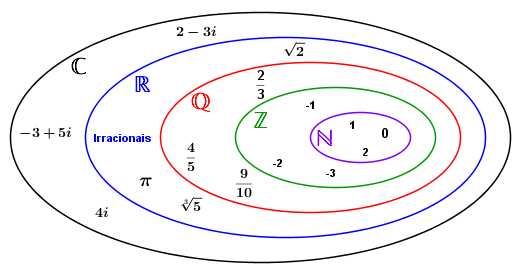
Resultado de imagem para conjuntos numericos

Fonte:http://www.centralexatas.com.br/matematica/conjuntos-numericos/formulas

Relações entre os conjuntos:

Existem diversas operações e conceitos que relacionam os conjuntos entre elas

Conjunto vazio {} ou Ø:

Não apresenta nenhum elemento. Representa o subconjunto de qualquer outro conjunto.

Relação de pertinência:

Indica que um certo número ou elemento pertence a um determinado conjunto. Pode ser usado para demonstrar que os mesmos não pertencem aos conjuntos. É válido essa notação somente para a relação entre elementos e conjuntos, nunca de conjuntos para conjuntos.

Exemplo:

N={2, 4, 6, 8, 10...}

*2 ∈ N ( 2 pertence ao conjunto N)

*3 ∉ N (3 não pertence ao conjunto N)

Conjunto unitário: Conjunto constituído por apenas um elemento.

Subconjuntos: Quando todos os elementos de um conjunto A pertencem a um conjunto B, é conclusivo que A é um subconjunto de B.

União: Dado dois conjuntos A e B, iria escrever todos os elementos em um novo conjunto união.

U ( união)

Exemplo

A={6,7}

B={8, 9, 10}

A U B={6, 7, 8, 9, 10}

Propriedade comutativa: A U B= B U A
Propriedade associativa: A U (B U C)= B U (A U C)
Propriedade neutra: A U {}= {}

Diferença entre conjuntos: A diferença entre conjuntos são os elementos de um conjunto que não pertencem a outro. Sempre é representada pelo menos e é também conhecido como conjunto diferença.
Dado dois conjuntos A e B, o conjunto diferença A-B indica somente os elementos que pertencem ao A, excluindo os de B e a intersecção entre eles.

Exemplo 1:
A={0, 1, 2, 3, 4 ,5}
B={5, 6, 7}

A-B={0, 1, 2, 3, 4}

Exemplo 2:
A={0, 1, 2, 3, 4 ,5}
B={5, 6, 7}

B-A={6, 7}

Conjunto complementar: Se relaciona com a diferença entre conjuntos. Dado dois conjuntos A e B, sendo que A ⊂ B, temos que:

A={2, 3, 5, 6, 8}
B={6,8}

O conjunto complementar CAB= A-B={2, 3, 5}. Neste exemplo, o conjunto complementar é basicamente todos os elementos que estão de fora do conjunto B.

Intersecção:

Conjunto formado pelos elementos comuns de dois ou mais conjuntos relacionados. Eles se unem, constituindo um conjunto intersecção.

H ∩ T={x ∈ T e x ∈ H}

Exemplo:

H={5, 10, 15, 20, 25, 30}

T={2, 4, 6, 8, 10, 12, 14, 16, 18, 20}

H ∩ T= {10, 20}

Exemplo 2

Y={2, 4, 6, 8, 10, 12, 14, 16, 18}

C={1, 3, 5, 7, 9, 11, 13, 15, 17}

Y ∩ C={}
(Quando isto ocorre, Y e C serão conjuntos disjuntos).

Propriedade comutativa: H ∩ T= T ∩ H
Propriedade associativa:H ∩ (T ∩ C)= T ∩( H ∩ C)
Propriedade de Idempotência=: H ∩ H= H
*H ∩ {}={}

Relação de inclusão: Utilizada para indicar quando todos os elementos de um conjunto pertencem ou não a outro.
Ela é representada por:
⊂ ( está contido)
⊃ ( contém)
⊄ ( não está contido)
⊅ (não contém)
Exemplo 1:

F={1, 4, 7, 10}
N={1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

Observamos que todos os elementos de F estão contidos em N, portanto, podemos afirmar que F⊂ N ou N ⊃ F.

Exemplo 2:

U={0, 2, 4, 6}

W={0, 2, 4, 8}

Como nem todos os elementos de U pertencem ao conjunto W, pode-se concluir que U⊄ W ou que W ⊅ U.

Relação de igualdade:
Dois conjuntos são iguais quando possuem os mesmos elementos.
Exemplo
O={0, 1, 2, 3, 4, 5}
P={5, 4, 3, 2, 1, 0}

Como P e O possuem os elementos. Pode-se dizer que P é igual a O (P=O).

Se os conjuntos não possuem todos os elementos iguais, eles são diferentes.

Exemplo 2:
L={2, 4, 8, 16, 32, 64}
B={0, 2, 4, 6, 8, 10}

Como L e B não possuem todos os elementos iguais, eles são diferentes. Portanto, L≠ B.
Por fim apresentarei as propriedades das relações de igualdade.
Propriedade reflexiva: Todo conjunto é igual a ele mesmo
Propriedade comutativa: Se A é igual a B, B é igual A

Agradecimentos:

Agradeço a todos que prestigiam a primeira postagem do meu novo blog. Espero que tenha ajudado alguém. Tudo que eu não tiver abordado sobre as operações entre os conjuntos nesta postagem, estará nas referências abaixo. Desculpem-me se as cores das letras mudaram um pouco, ocorreram problemas técnicos.,

Quaisquer sugestões de melhorias no blog e de novos conteúdos, escrevam nos comentários. Se tiverem dúvida, escrevam também.

No dia 15 de outubro irei lançar a próxima postagem com exercícios.