Questão 1) Um cone circular reto tem 12 cm de raio e 16 cm de altura. Determine a área total e lateral deste cone.
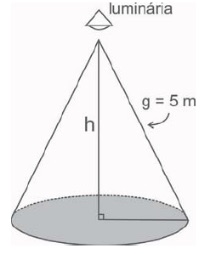
Sabendo - se que a luminária deverá iluminar uma área circular de 28,26 m², considerando
π (pi)= 3,14, a altura será igual:
π (pi)= 3,14, a altura será igual:
a) 3 m
b) 4 m
c) 5 m
d) 9 m
e) 16 m
Questão 3) (UECE)- Um cilindro circular reto de altura 7 cm tem volume igual a 28π cm³. A área total desse cilindro, em cm², é:
a) 30π
b) 32π
c) 34π
d) 36π
Questão 4) (USF-SP)- Um cilindro circular reto, de volume 20π cm³, tem altura de 5 cm. Sua área lateral , em centímetros quadrados, é igual a:
a) 10π
b) 12π
c) 15π
d) 18π
e) 20π
Questão 5) Uma esfera têm 25π cm² de superfície. Em quanto devemos aumentar o raio para que a área passe a ser 64π cm²?
Questão 6) Uma esfera está inscrita num cubo cuja aresta mede 20 cm. Calcule a área superfície esférica.
Questão 7) Qual é a área total de um cubo cujas arestas medem 15 centímetros?
a) 550 cm²
b) 1350 cm²
c) 1450 cm²
d) 1800 cm²
d) 1800 cm²
e) 1850 cm²
Questão 8) Qual a diferença entre as áreas de dois cubos que possuem arestas iguais a 10 e a 25 cm, respectivamente?
a) 3150 cm²
b) 3250 cm²
c) 3350 cm²
d) 3450 cm²
e) 3550 cm²
Questão 9) Um armário, com a forma de dimensões 0,5 m; 2,5 m e 4 m, deve ser pintado. O rendimento da tinta empregada é de 5 m² por litro. Determine a quantidade de tinta necessária para pintar toda a parede interna do armário.
Resoluções:
Questão 1)
Dados:
h= 16 cm
r= 12 cm
I) Primeiramente, determinaremos a geratriz do cone.
g²= r²+ h²
g²= 12² + 16²
g²= 144 + 256
g²= 400
g=√400
g= 20 cm
II) Agora basta substituirmos as medidas do cone nas fórmulas:
* Área lateral
Al= πrg
Al= π • 12 • 20
Al= π • 240
Al= 240π cm²
*Área total
At= πr(r + g)
At= π • 12 • (12 + 20)
At= 12π • 32
At=384π cm²
Questão 2)
Dados:
g=5 m
Ab= 28,26 m²
I) Como sabemos que a área circular do cone da imagem é 28,26 m^2 e considerando π= 3,14 , o raio desta circunferência será dado por:
Ab= πr²
3,14 • r^2= 28,26
r²= 28,26
3,14
r²= 9
r=√9
r= 3 m
II) Agora podemos determinar a altura ideal para se instalar a luminária pelo teorema de Pitágoras.
g²=r²+ h²
5²= 3² + h²
25= 9 + h²
h²= 25 -9
h²= 16
h= √16
h= 4 m
Resposta: Item b
Questão 3)
Dados:
V= 28π cm³
h= 7 cm
I) Sabendo- se que o volume do cillindro é dado por V= π • r² • h, o raio deste sólido será igual
π • r² • 5= 20π
5π • r²= 28π
r²= 20π
5π
r²= 4
r= √4
r= 2 cm
II) Agora que conhecemos as medidas da altura e do raio do cilindro, podemos determinar a área total do mesmo substituindo os valores do mesmo na fórmula abaixo.
At= 2πr(r+h)
At= 2 • π • 2 • (2 + 7)
At 4π • 9
At= 36π cm²
Resposta: Item d
Questão 4)
Dados:
V= 20π cm³
h= 5 cm
I) Sabendo- se que o volume do cillindro é dado por V= π • r² • h, o raio deste sólido será igual
π • r² • 7= 20π
7π • r²= 28π
r²= 28π
7π
r²= 4
r= √4
r= 2 cm
II) Agora que conhecemos as medidas da altura e do raio do cilindro, podemos determinar a área total do mesmo substituindo os valores do mesmo na fórmula abaixo.
At= 2πrh
At= 2 • π • 2 • 5
At 4π • 5
At= 20π cm²
Resposta: Item e.
Questão 5)
Dados:
Ao= 25π cm²
A= 64π cm²
I) Primeiramente, devemos determinar o raio da esfera com antes de aumentar sua área.
A=4 • π • r²
4 • π • r²= 25π
r²= 25π
4π
r²= 6,25
r= √6,25
r= 2,5 cm
II) Em seguida, devemos calcular o raio da esfera depois de seu aumento de área.
4 • π • R²= 64π
R²= 64π
4π
R²= 16
R= √16
R= 4 cm
III) Como conhecemos o valor do raio inicial e final desta esfera, a variação do seu raio corresponderá a:
∆R= R -r
∆R= 4 - 2,5
∆R= 1,5 cm
Resposta: A variação do raio será igual a 1,5 cm.
Questão 6)
I) Visto que a esfera está inscrita em um cubo com arestas que medem 20 cm, podemos concluir que o raio da esfera será metade da medida da aresta do cubo. Logo, a esfera possui um raio igual a 10 cm.
A= 4 • π • r²
A= 4 • π • 10²
A=4π • 100
A=400π cm²
Resposta: A superfície esférica desta esfera é igual a 400π cm^2
Questão 7)
I) Como sabemos que o cubo possui arestas com medida igial a 15 cm
Basta substituir esse valor na fórmula abaixo para determinarmos a sua área.
A= 6 • L²
A= 6 • 15²
A= 6 • 225
A= 1350 cm²
Resposta: Item b.
8)
I) Sabendo que um dos cubos possui arestas com medida igual 25 cm e o outro tem arestas com medida igual a 10 cm, devemos calcular a área de cada um deles primeiramente.
*Área do menor cubo
A1= 6 • 10²
A1= 600 cm²
*Área do maior cubo
A2= 6 • 25²
A2= 3750 cm²
II) A variação de área corresponderá a:
A2 - A1= 3750 - 600
A2 - A1= 3150 cm²
Resposta: Item a.
9)
Dados:
a=0,5 m
b= 2,5 m
c= 4 m
I) Primeiramente, devemos determinar a área interna do armário.
A=2 • ( ab + ac + bc)
A= 2 • ( 0,5 • 2,5 + 0,5 • 4 + 2,5 • 4)
A= 2 • ( 1,25 + 2 + 10)
A= 2 • 13,25
A= 26,5 m²
II) Como sabemos que a tinta tem um rendimento de 5 m^2 por litro e a área interna do armário, a quantidade total de tinta gasta será:
5
Resposta: A quantidade de tinta gasta na pintura deste armário será igual a 5,3 litros.
Referências:
3-http://questoesdevestibularnanet.blogspot.com/2013/11/questoes-resolvidas-de-vestibular-sobre.html
Nenhum comentário:
Postar um comentário