Desafios de Física 2.0

Questão 1) (ITA 2019) Considere duas partículas de massa m, cada qual presa numa das pontas de uma corda, de comprimento l e massa desprezível, que atravessa um orifício de uma mesa horizontal lisa. Conforme mostra a figura, a partícula descreve um movimento circular de raio r e velocidade angular ω₁. A partícula suspensa também descreve esse mesmo tipo de movimento, mas com uma velocidade angular ω2, estando presa a uma mola de constante elástica k e comprimento natural desprezível, mantida na horizontal. Sendo g o módulo da aceleração da gravidade e θ o ângulo de suspensão da corda com a vertical, a razão (ω2/ω1)² é dada por:

Questão 2) (ITA-2015) Uma pequena esfera metálica, de massa m e carga positiva q, é lançada verticalmente para cima com velocidade inicial Vo em uma região onde há um campo gravitacional elétrico de módulo E, apontando para baixo, e um gravitacional de módulo g, ambos uniformes. A máxima altura que a esfera alcança é:

a) V0²/2g

b)qE/mV0

c) V0/qmE

d)mV0²/2(qE + mg)

e)√[3mEqV0/8g]

Questão 3) (ITA 2007)

Questão 4) (ITA 2007)

Resoluções:

Questão 1) (ITA 2019)

I) Primeiramente, temos a seguinte relação para a força centrípeta da partícula de cima:

Fcp=T=m(ω1)²r (i)

II) Para a partícula de baixo, temos:

P= T cos θ => T= mg/cos θ (ii)

Igualando i e ii

m(ω1)²r= mg/cos θ

(ω1)²r= g/cos θ

(ω1)²=g/(r • cos θ) (iii)

III) Ainda na partícula de baixo, temos:

Tsen θ + kR= m(ω2)²R (iv)

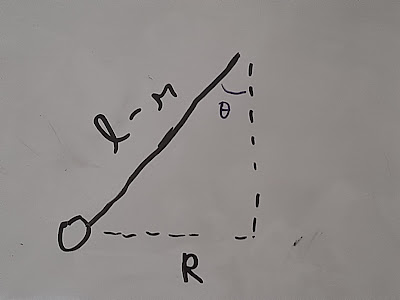
Da figura abaixo, descobrimos que:

R/(l - r)= sen θ

R= (l - r)sen θ (v)

(v) em (iv)

Tsen θ + kR= m(ω2)²R 

Tsen θ + k(l - r)sen θ= m (ω2)²(l - r)sen θ 

Simplificando

T + k(l - r)= m(ω2)²(l - r) => (ω2)²=[T + k(l - r)]/[m(l - r)] (vi)

IV) Dividindo (vi) por (iii)

(ω2/ω1)² ={[(mg/cos θ) + k(l - r)]}/m(l - r)}/[g/(r • cos θ)]

(ω2/ω1)² = {[(mg/cos θ) + k(l - r)]}/m(l - r)} • [(r • cos θ)/g]

(ω2/ω1)² = r • [(mg + k(l - r)cos θ)/mg(l - r)]

Resposta: (ω2/ω1)² = r • [(mg + k(l - r)cos θ)/mg(l - r)]. Item a

Questão 2) (ITA 2015)

I) Visto que as forças atuantes no sistema são a gravitacional e a elétrica, ambas apontando para baixo, teremos a seguinte aceleração para o sistema:

Fr= Fe +P

m • a_r= qE + mg

a_r= (qE + mg)/m

II) Sabe-se que a velocidade vertical da esfera será nula na altura máxima:

V²= V0² + 2a_rHmáx  (tomando como positivo o referencial para cima)

0=V0² - 2[(qE + mg)/m]Hmáx

2[(qE + mg)/m]Hmáx= V0² 

Hmáx= V0²/2[(qE + mg)/m]

Hmáx= mV0²/2(qE + mg)

Resposta:mV0²/2(qE + mg) Item d

Questão 3) (ITA 2007)

I) Primeiramente, as duas primeiras molas de constante elástica K1 encontram-se em paralelo e, sendo assim, equivalem uma mola de constante elástica Keq1.

Keq1= K1 + K1= 2K1

II) As três molas de constante elástica K2 também encontram-se em paralelo e, sabendo disso, descobrimos que equivalem a uma mola de constante elástica Keq2.

Keq2= K2 + K2 + K2= 3K2

III) Nesse caso, o sistema reduz-se a um sistema de duas molas em série com constantes elásticas Keq1 e Keq2, como na figura abaixo:

A constante elástica k da mola osciladora do sistema será:

K= (1/Keq1) + (1/Keq2)= (Keq2 + Keq1)/(Keq1 • Keq2)

K=( 3K2 + 2K1)/(2K1 • 3K2)=(2K1 + 3K2)/(6K2K1)

IV)  A frequência de oscilação do sistema fica igual a:

f=(1/2π) √(K/m)

f=(1/2π) √{[((2K1 + 3K2)/(6K2K1)]/m}

f= (1/2π) √{6K1K2/[m(2K1 + 3K2)]}

Resposta: f= (1/2π) √{6K1K2/[m(2K1 + 3K2)]}

Questão 4) (ITA 2007)

Por definição, a imagem virtual é aquela que fica atrás do espelho. Sabendo disso, infere-se que a distância de B a imagem é representada pelo segmento A'B na figura abaixo

Lembrete: todas as medidas estão em metros

Pelo teorema de Pitágoras no triângulo A'TB na figura:

A'B²= 5² + (2 + 3)²= 5² + 5²= 2 • 5²

A'B²= 2 • 5²  => A'B=5√2 m

Resposta: A'B=5√2 m

Agradecimentos:

Agradeço a todos que prestigiaram o meu blog e espero que gostem das atuais e futuras postagens.  

Quem tiver dúvidas, pode comentá-las. Espero ter ajudado, principalmente em meio a esta situação da pandemia.